Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.1 - Ex. 8

  1. O que você pode dizer sobre o gráfico de uma solução da equação y ' = x y 3 quando x está próximo de 0 ? E se x for grande?
  2. Verifique que todos os membros da família y = c - x 2 - 1 2 são soluções da equação diferencial y ' = x y 3
  3. Trace vários membros da família de soluções na mesma tela. Os gráficos confirmam o que você predisse na parte (a)?
  4. Encontre uma solução para o problema de valor inicial y ' = x y 3 y 0 = 2

Passo 1

  1. Precisamos tirar conclusões sobre o gráfico da solução de y ' = x y 3 quando x está próximo de 0 e quando x for bem grande, sem de fato olhar para o gráfico. Bom, quando x é próximo de 0 , a derivada também é próxima de 0 , e portanto a inclinação é paralela ao eixo X .

Se x for "grande" temos que a derivada da função é igual ao próprio valor da função naquele ponto, ou seja dá algum número vezes algo "grande", então podemos entender que esse produto seria grande, portanto, a derivada tem um valor grande. A consequência disso é que quando você estiver muito a direita no gráfico a função tem uma variação grande e a sua reta tangente tem uma inclinação muito alta.

Passo 2

(b) Queremos verificar que as equações do tipo y = c - x 2 - 1 2 são soluções de y ' = x y 3 .

Primeiro vamos derivar y ,

y = C - x 2 - 1 2

y ' = x C - x 2 3 2

x C - x 2 3 2 = x   C - x 2 - 3 2 )  

x C - x 2 3 2 = x C - x 2 3 2

Desse modo, concluímos que y = c - x 2 - 1 2 são soluções de y ' = x y 3 .

Passo 3

(c)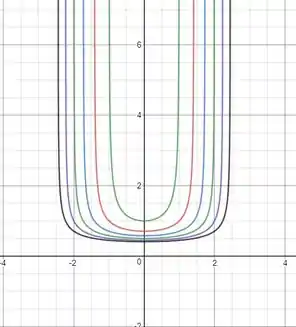

Sim, o gráfico confirma o que foi dito no item (a).

Passo 4

  1. Precisamos achar uma solução para o PVI, tal que y 0 = 2

Utilizando o item (b), sabemos que y = C - x 2 - 1 2 é uma solução, portanto temos que encontrar agora o valor da constante C .

y 0 = 2

y 0 = C - 1 2 = 2

  1 C 1 2 = 2

C = 1 4

Então uma solução é y = 1 4 - x 2 - 1 2

Resposta

(d)         y = 1 4 - x 2 - 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a solução completa da equação diferencial (14) d ² u d v ² = t g vs e c ² v ² ² ² .
Ache a solução completa da equação diferencial (7) d u d v = 3 v ( 1 + u 2 ) u .
Ache a solução completa da equação diferencial (11) d ² y d x ² = 5 x 2 + 1 ² ² .
Ache a solução completa da equação diferencial dada, determinada pelas condições iniciais (17) d y d x = c o s 3 x s e n 2 y ; y = π 3q u a n d ox = π 2 .
Ache a solução completa da equação diferencial dada, determinada pelas condições iniciais (19) d ² u d v ² = 4 ( 1 + 3 v ) ² ; u = - 1e d u d v = - 2q u a n d ov = - 1 ² ² ² .