Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 27
A função densidade conjunta para um par de variáveis aleatórias e é
(a) Determine a constante .
(b) Determine .
(c) Determine .
Passo 1
Fala, pessoal! Tudo bem?
A questão dá a função densidade de probabilidade
E pede para que a gente determine algumas coisas.
A parte a) pede a constante , que a gente vai achar partindo do princípio de que a integral dupla de de até é igual a 1:
A parte b) pede para acharmos o valor de , ou seja, a probabilidade de e serão no máximo igual a 1. Ou seja, vamos calcular a integral dupla da função, mas colocando essas condições nos limites de integração.
Finalmente, a parte c) pede , ou seja, a probabilidade de serem menores que 1. Para isso vamos entender qual região está sendo descrita e usá-la para acharmos novos limites de integração para nossa função densidade de probabilidade.
Vamos lá?
Passo 2
(a) Galera, pra determinar , lembre-se que temos que ter:
Calculando a integral, obtemos:
Como o enunciado dá que:
Para um intervalo de:
Esses são nossos limites de integração. Separando nossa integral num produto de integrais, cada qual com sua variável de integração:
Agora integrando cada uma:
Podemos aplicar os limites de integração:
Então, como vimos no passo 1:
Isolando :
Chegamos no nosso valor procurado!
Passo 3
(b) Agora vamos calcular a probabilidade de e serão no máximo igual a 1. Então, nossos limites são:
Aplicando na nossa integral dupla:
Vamos resolver a integrais:
Aplicar limites de integração:
Temos então:
Passo 4
(c) , ou seja, a probabilidade de serem menores que 1. Para conseguirmos escrever a integral, vamos esboçar qual será a região de integração:
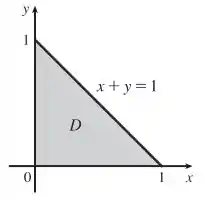
É a região onde os valores de é menor que 1
Vamos descrever essa região como uma região do tipo , onde está entre duas constantes e está entre duas funções. Podemos ver que:
E isolando na equação da nossa reta:
É:
Então nosso intervalo fica:
Assim, teremos:
Vamos começar a integrar por dentro em , tratando como constante:
Aplicando os limites de integração:
Simplificando:
Podemos finalmente integrar em :
Aplicando os limites:
Temos:
Resposta
(a)
(b)
(c)