Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.5 - Ex. 8
Determine a massa e o centro de massa da lâmina que ocupa a região e tem função densidade .
é delimitada por e ;
Passo 1
Falaa, turma!
Nessa questão temos que encontrar a massa e o centro de massa de uma lâmina.
As informações que temos são a região que ela ocupa e a função densidade .
Com isso, conseguimos calcular o que precisamos.
Pra massa:
Pra coordenada do centro de massa:
Pra coordenada do centro de massa:
Vamos começar esboçando a região , pra conseguir transformar essas integrais em integrais iteradas, e ai calculamos (de dentro pra fora).
Percebe que a primeira a ser calculada tem que ser a massa, porque as coordenadas do centro de massa dependem dela!
Passo 2
A região é limitada pela curva
Que é a mesma coisa que
Só que só na região onde .
Além disso, é limitada também pelas retas:
Desenhando isso, chegamos na região:
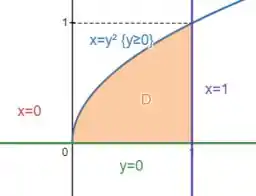
Bom, nossa região está a direita da curva (ou seja, é maior que isso) e a esquerda de ( é menor que isso):
Já em relação a , estamos entre e :
Como os limites de dependem de , integramos primeiro em função de !
Agora já temos todas as informações pra calcular as integrais.
Passo 3
Primeiro vamos calcular a massa:
Começamos integrando em função de , considerando como constante:
Substituindo nos limites:
Agora integrando em função de :
Passo 4
Agora vamos calcular , pra saber qual é o centro de massa :
Começamos integrando em função de , com constante:
Aplicando os limites:
Integrando em função de :
Simplificando:
Passo 5
Só falta calcular :
Primeiro integramos em função de , mantendo constante:
Calculando nos limites de integração:
Por último, integrando em função de :
Então,