Função Afim
Teoria
Fala aí, você chegou no Responde Aí! E vamos lá bater um papo sobre Função Afim.
O que é Função Afim?
Nós sempre vamos pensar nas funções com aquela definição que vimos antes: TODO elemento do domínio se relaciona a um ÚNICO elemento do contradomínio.
Funções afim são funções que tem a seguinte forma:
Onde
Ou seja, todas as funções abaixo são Funções Afim:
Ou seja, sempre serão funções que lembram muito um polinômio de grau 1 ou grau 0 (o maior valor de expoente que vai estar junto do “x” é 1 ou 0).
Gráfico da Função Afim
Vamos montar o gráfico de uma função afim para estudar como funciona essa coisa toda.
O gráfico da Função Afim sempre é uma reta. Então para fazer o seu gráfico só vamos precisar de dois pontos! Vamos ver num exemplo.
Exemplo: Desenho o gráfico de
Passo 1: Vamos descobrir o valor de
Passo 2: Vamos descobrir o valor de
Passo 3: Num gráfico a gente marca os dois pontos:
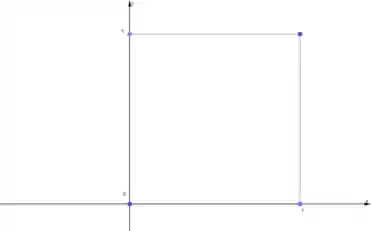
Passo 4: E agora a gente só precisa ligar os pontos com uma reta!7
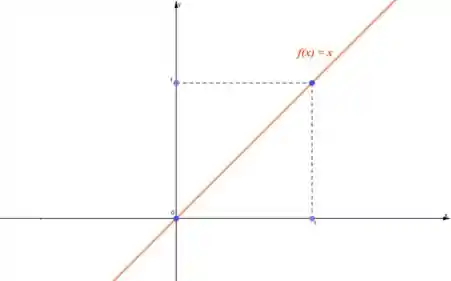
Interceptando os eixos
O zero de uma função é o valor de
Já a interseção com o eixo
Ou seja, quando
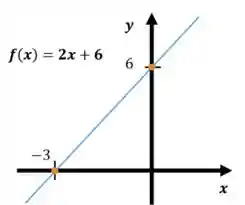
Exemplo: Encontre o zero da função e a interseção com
Passo 1: Para encontrar o zero da função é só igualar a função a zero:
Ou seja, a função é igual a corta o eixo
Passo 2: A função intercepta o eixo y quando
Ou seja, a função é igual a corta o eixo
Videoaula
Quer saber ainda mais sobre Função Afim? Então olha essa nossa videoaula que ensina tudo que você precisa saber
Não para por aí! Olha aqui em baixo e confere uns exercícios resolvidos 👇
Gráfico da Função Afim
Interceptando os eixos
Videoaula
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine os zeros das funções
Passo 1
Vamos lá!! Queremos encontrar o zero das funções, ou seja, o valor de que faz com que a função seja igual a zero.
Lembrando que quando falamos qua a função será um determinado valor, estão falando do encontrado.
Então, para fazer isso, basta fazermos ! Bora pras continhas!
Passo 2
- Na letra (a) temos a função:
- Vamos utilizar o mesmo raciocínio na letra (b). Fazendo
Fazendo
Teremos:
Vamos só trocar de lado pra ficar mais corfortável pra resolver:
Para encontrar o valor de passamos o número para o outro lado ele estava somando, e passa subtraindo.
Agora, vamos deixar o sozinho passando o número 5 que estava multiplicando ele, para o outro lado dividindo:
Realizando a divisão, temos
Ou seja, o zero da função é .
OBS: Pra termos certeza que fizemos a coisa certa, nós podemos testar, pra isso a gente pega a função original e substitui o valor de que acabamos de encontrar como raiz. Veja:
Com :
Viu, deu certinho, quando o , realmente a função vai a zero!
Passo 3
Temos
Mudando de lado:
Assim, o número mudará de lado dividindo.
Repara que o que munda quando jogamos o para o outro lado é a operação, e não o sinal. Nesse caso, ele estava multiplicando o e passa para o outro lado dividino que é a operação inversa da multiplicação. Por isso ele vai com o seu sinal de menos. Ok? Nós só mudamos o sinal quando ele está somando ou subtraindo!
Assim:
EPAAAAA! Mas teremos o número dividido por ... O zero dividido por qualquer número é zero!
Assim, o zero da fnção é !
Beleza?!
Resposta
Exercício Resolvido #2
Elaboração Própria
Diga se as funções abaixo são crescentes ou decrescentes:
Passo 1
BORA TIMEEE!! Para classificarmos as funções afins como crescentes ou decrescentes precisamos lembrar que ela tem esse formato aqui:
E elas terão as seguintes carinhas:
Show de bola?! Então vamos analisar cada caso!
Passo 2
a) Na letra (a) temos a função . Quem é o aqui nesse caso? Se você reparar
Então,
Como nosso é maior que zero, a função é crescente!!
Passo 3
b) Vamos utilizar o mesmo raciocínio!! Temos a função . Nesse caso, quem será o nosso ?
Você concorda que o nosso ? Assim,
Portanto, a função é descrescente!
Passo 4
c) Pra terminar, vamos analisar a função . Tá meio diferente a carinha dessa função, né?! Mas não se assuste que vai ser mais fácil e rápido do que você imagina!!!
Se você reparar, o está multiplicando o , olha:
E nesse caso não teremos o termo “b” da nossa função. Temos algo do tipo
Como o “” é o termo que acompanha o , o nosso aqui é
Ou seja, a função é decrescente!
Resposta
- Crescente
- Decrescente
- Decrescente
Exercício Resolvido #3
UFPI
A função real de variável real, definida por , é crescente quando:
Passo 1
Opaaaa! Antes de tudo vamos lembrar como classificamos as funções em crescentes ou decrescentes?
Show de bola?! Vamos então identificar o da função e verificar quando será crescente.
Passo 2
O termo “” da função é aquele que sempre acompanha o , certo? No caso da nossa função
O termo que acompanha o é
E para a função ser crescente esse termo que acompanha o precisa ser maior que zero. Assim,
Veja que aqui temos um inequação, é parecido com as equações, mas ao invés de termos o sinal de igual temos o sinal de maior . Pra resolver fazemos de forma bem parecida com a o que já fazemos nas equações. Veja:
Podemos passar o três para o outro lado invertendo o sinal
Como temos o sinal de menos em ambos os lados, vamos multiplicar tudo por para sumir com o sinal de menos. Quando fizermos isso, o sinal da desigualdade irá inverter. Repare:
Beleza?!
Agora é só passar o que está multiplicando o para o outro lado dividindo. Assim,
E prontinho!
Ouuu seja, para a nossa função ser crescente,
Resposta
Letra (B)
Exercício Resolvido #4
Elaboração Própria
Considere a função . Qual o valor de para que ?
Passo 1
Vamos láá!!! Temos a função e queremos encontrar o valor de de forma que , certo? Como podemos fazer isso?
Basta igualarmos
E encontrar o valor de !!
Passo 2
Vamos então isolar o da equação
Beleza?!
Dessa forma, o passará para o outro lado invertendo o sinal
E agora o passará para o outro lado dividindo
Portanto, o valor de para que é !
Resposta
Exercício Resolvido #5
Elaboração Própria
Diga se as afirmações abaixo são verdadeiras ou falsas:
- O coeficiente angular (taxa de variação) da função é ;
- O coeficiente Linear da função é ;
- A função é crescente;
- No plano cartesiano, o eixo das ordenadas é equivale ao , enquanto que o eixo das abscissas corresponde ao .
Passo 1
Fala Aíí!! Vamos analisar cada uma das afirmações e verificar quais são verdadeiras e quais são falsas!
Na letra (a) temos a afirmação “O coeficiente angular (taxa de variação) da função é . Vamos lembrar o que é o coeficiente angular de uma função? Em uma função, , o “” é chamado de coeficiente angular ou taxa de variação e está ligado a inclinação da reta em relação ao eixo .
Ou seja, na função o nosso coeficiente angular será o número , e não o como informado na afirmação! Assim, a afirmação é falsa!
Passo 2
b) A letra (b) fala sobre coeficiente linear de uma função. O coeficiente linear de uma função será o termo independente:
Portanto, na função o coeficiente linear é o termo ! Ou seja, a afirmação é verdadeira!!
Passo 3
c) A afirmação da letra (c) é “A função é crescente”. Uma função será crescente quando
Beleza?! Aqui como o nosso , então a função será decrescente. Ou seja, a afirmação é falsa!!
Passo 4
d) A última afirmação “No plano cartesiano, o eixo das ordenadas é equivale ao , enquanto que o eixo das abscissas corresponde ao fala sobre os eixos do plano cartesiano. Vale lembrar que
E na afirmação da letra (d) fala exatamente o contrário, rs. Então a afirmação é falsa!
Resposta
- Falsa
- Verdadeira
- Falsa
- Falsa
Exercício Resolvido #6
AV1 Estácio de Sá
Dada uma função , determine o valor de para que se tenha .
Passo 1
Substitua o valor de na função
Passo 2
Substitua o valor de
Resposta
Agora ficou fácil, fácil !!! É só escrever a equação substituindo o valor de .
Exercício Resolvido #7
Elaboração Própria
Dado os pontos e determine a respectiva reta que passa por P e Q.
Passo 1
Escreva a equação geral da reta:
Passo 2
Substitua os pontos dados para encontrar duas equações. Aqui caberá lembrar que um ponto é um par ordenado .
Equação para o ponto :
Equação para o ponto :
Passo 3
Agora você deverá isolar uma variável da equação (1) e substituir na equação (2).
Substituir (3) em (2):
Por último, substitua na equação (1) ou (2). Tanto faz, você pode fazer o teste para comprovar o resultado.
Conhecendo os valores de e , basta escrever a função.
Resposta
Exercício Resolvido #8
Elaboração Própria
A função é do 1º grau. Escreva a função se e
Passo 1
Em primeiro lugar vamos escrever a equação do 1º grau na forma geral:
(Daria no mesmo se você escrevesse ou ou quaisquer outras letras)
Passo 2
Agora vamos escrever as relações substituindo os dados do enunciado
Como os valores de e são conhecidos vamos substituir nas equações (1) e (2)
Passo 3
Basta isolar uma variável em umadas equações anteriores e substituir na outra equação
Substituir em (4) para obter :
E subititua em (3), (4) ou (5):
Por fim escrevemos a equação procurada, onde a e .
Resposta
Exercício Resolvido #9
Elaboração Própria
A medida que o ar seco move-se para cima, ele se expande e esfria. Se a temperatura do solo for e a temperatura a uma altitude de 1 km for de , expresse a temperatura em como função da altitude em Km, supondo que um modelo linear seja apropriado.
Passo 1
Para comerçarmos a resolver isso você deve saber o que é um modelo linear. Pulo do gato!!!
é um modelo linear, porque representa uma reta. Quer dizer que a temperatura varia em função da altura de forma linear.
Logo, vamos escrever a equação utilizando as variáveis que o problema sugeriu.
Você deve estar se perguntando, como chegar nisso sozinho??
Note que é a temperatura que varia conforme muda a altura , pronto é só isso. Agora voltaremos ao enunciado e vamos determinar o valor de .
Passo 2
O enunciado diz que quando está na altura do solo, ou seja,
Também é dado que em , a temperatura é
Conhecendo os valores de e , basta escrever a função.
Resposta
Exercício Resolvido #10
Fundamentos da Matemática Elementar Vol. 1 Gelson Iezzi
Estudar segundos os valores do parâmetro , a variação(crescente, decrescente ou constante) das funções abaixo:
Passo 1
a)
Bom, nessa função afim temos que .
Portanto, temos que usar a definição de função crescente, decrescente e constante.
Se:
- Então a função é crescente.
- Então a função é decrescente.
- Então a função é constante.
Passo 2
b)
Nessa função, temos
Então, se:
- Então a função é crescente.
- Então a função é decrescente.
- Então a função é constante.
- Então a função é crescente.
- Então a função é decrescente.
- Então a função é constante.
- Então a função é crescente.
- Então a função é decrescente.
- Então a função é constante.
Passo 3
c)
Nessa função temos
Então, se:
Passo 4
d)
Nessa questão temos que fazer um pouco de manipulação.
Bom,
Agora só precisamos nos preocupar com o valor de , não ligue para o valor de b mesmo que tenha um no meio.
Então, se:
Resposta
a)
b)
c)
d)