Função Exponencial
Produzido por Erick PinhoTeoria
Expoentes e Raízes
Vou confessar uma coisa a você, CANSEI DE SER EXPERT NO RESPONDE AÍ. Vou trabalhar agora como empregado doméstico e quero oferecer meus serviços a VOCÊ! (Olha que privilégio, rs)
Agora olha como eu sou bonzinho, no primeiro mês eu quero ganhar míseros 2 REAIS, isso mesmo, 2 REAIS.
Maaaas tenho minhas exigências, quero que você assine um contrato de 2 anos e que todo mês você DOBRE o meu salário.
Show, né?
Prometo que faço de tudo, lavo, passo, arrumo casa, faço sua comida preferida, escolho as melhores séries pra você assistir, de quebra, ainda te ajudo em pré-cálculo hahaha
E aí, vai me contratar ou não?
Vou te dar uns 5 segundos pra pensar!!!
.
.
.
.
Pensou?
Vamos fazer umas continhas, pra saber quanto vou ganhar em cada mês:
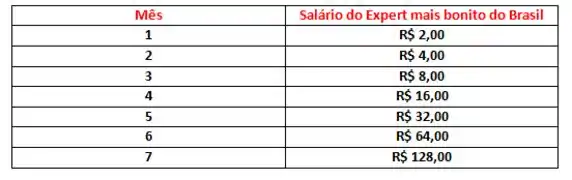
Fala aí, molezinha né?
Somando o meu salário nos primeiros 7 meses, a gente vai ter míseros 254 reais. Nem aperta o orçamento né?
Mesmo sendo universitário, dá pra pagar! (Ou não =D #descubra)
Vamos entender o que está acontecendo aqui na nossa tabela...
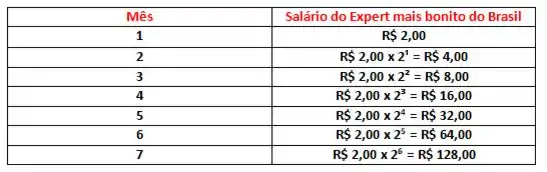
O que a gente fez foi criar um padrão, certo?
Um jeito de economizar esforço. Ao invés de escrevermos:
Podemos escrever:
(Lindo)
Agora, tente calcular o quanto eu vou ganhar no último mês de contrato...
.
.
.
Vamos usar a mesma ideia, eu te disse que o contrato vai ser de 2 anos = 24 meses.
Ou seja, teremos que:

Se você ficou com essa cara aí, não se assusta! Coisas exponenciais realmente crescem MUITO, MUUUUUUITO RÁPIDO. A ponto de eu estar ganhando 128 reais no 7º mês e aquele absurdo no 24º rs
ACHO QUE ALGUÉM DESISTIU DE ME CONTRATAR, SÓ ACHO HAHAHAHA
![]() Ah, era brincadeira, tá? Tô muito feliz aqui falando com você, não quero trocar de emprego!
Ah, era brincadeira, tá? Tô muito feliz aqui falando com você, não quero trocar de emprego!
A Função Exponencial
Vamos entender melhor o processo agora, a função exponencial é uma função da forma:
Onde é um número real positivo que nós chamamos de base. O argumento é chamado de expoente. Basicamente o que essa função faz é pegar a base e multiplicar por si mesma vezes. Por exemplo:
Se fizermos o :
A função exponencial também pode vir multiplicada por uma constante qualquer, por exemplo:
Daí, substituindo alguns valores teríamos:
E é basicamente isso que precisamos saber do escopo da função exponencial.
Domínio
Vamos tomar como exemplo a função
E vamos considerar aqui diferentes valores de pra ver o que acontece com a função:
- e inteiro:
- e não inteiro:
- :
Neste caso, temos um número positivo multiplicado por ele mesmo vezes. Não há nenhum mal nisso e não haverá indeterminação.
Neste caso, podemos ter uma raiz aparecendo, uma vez que, por exemplo:
Porém, como definimos que na função exponencial, a raiz será sempre positiva, e novamente está tudo ok!
Nesse caso também não tem nenhum problema, já que sempre que o expoente é negativo, descemos a potência para o denominador, por exemplo:
A única coisa que poderia dar problema aqui é se tivéssemos zero embaixo, já que não conseguimos dividir por zero. Porém, como , esse denominador nunca será zero, então também não haverá indeterminação ou singularidade.
Logo, se o pode ser qualquer coisa, temos que o pertence aos reais, ou seja, o domínio é:
Gráfico
O gráfico da função exponencial depende da sua base. No caso, existem duas possibilidades que vamos estudar. A primeira é se a base for maior que :
O outro caso é se a base estiver entre zero e um:
No primeiro caso, o gráfico da função é uma crescente que corta o eixo no ponto , ou se a função estiver sendo multiplicada por uma constante “”.
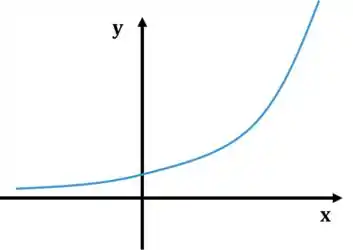
No segundo caso, a função é uma decrescente que também corta o eixo no mesmo ponto de antes.
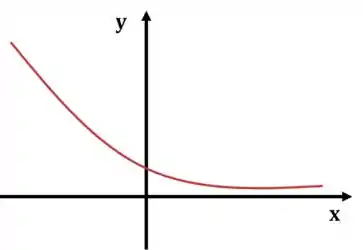
Repare que a função, em ambos casos, se aproxima cada vez mais de zero, mas nunca chega a esse valor.
Imagem
Vimos que o domínio é composto por todo o conjunto dos números reais, mas a imagem, que é o conjunto dos valores que o assume, vai ser limitado. À princípio, pode parecer estranho de perceber, mas note:
A função é a mesma coisa que multiplicar um número positivo () por si mesmo várias vezes. Então eu lhe pergunto, tem como o resultado dar negativo? A resposta é não, já que a multiplicação de números positivos, sempre dá outro número positivo.
E zero? Pode dar zero? Como o é diferente de zero, também não tem como. Portanto:
Dessa forma, a imagem é qualquer número real positivo, como podemos perceber nos gráficos onde a função está representada apenas acima do eixo !
Podemos representar esse conjunto de três maneirais:
O sinal de mais em cima do indica que são os reais positivos incluindo o zero. Nós fazemos a operação de excluir o elemento zero (), pois ele não faz parte da imagem.
Já o indica que são os reais positivos excluindo o zero, que é exatamente a imagem da função!
Número de Euler
Uma função muito recorrente no cálculo é a função exponencial de base .
Esse é um número irracional assim como nosso amiguinho . Seu valor é aproximadamente:
Existem diversas situações associadas ao número e que serão discutidas mais para frente.