Função Logarítmica
Produzido por Erick PinhoTeoria
O logaritmo
FALAAAAAAA AÍ, TUDO BEM COM VOCÊ?
Se a resposta for não, isso pode estar intimamente associado à palavra LOGARITMO.
Se você tem trauma com o famoso , muito provavelmente você carrega ele desde a época do Ensino Médio. Mas relaxa, o logaritmo não precisa ser esse bicho papão que parece.
O logaritmo sempre está associado a um expoente! Então vamos falar um pouquinho dos expoentes, aqui segue um exemplo:
Neste exemplo, nós temos uma base que está elevada ao quadrado, ou seja, nosso expoente é . Para fazer essa conta, multiplicamos o por ele mesmo duas vezes e chegamos ao resultado, que é o .
Agora eu vou mudar um pouco a pergunta. O que acontece se eu quiser saber quantas vezes o número (base) foi multiplicado até chegar a ? Para representar isso, eu vou usar um logaritmo. Desta forma, teremos
E resolvendo, encontramos o , uma vez que .
Resumindo, quero que você sempre pense que LOGARITMO = EXPOENTE.
A função logarítmica
Então a pergunta que sempre vamos fazer quando surgir um logarítmo é:
“A base elevada a qual número tem como resultado o?"
E a função logarítmica é justamente a representação dessa ideia e tem como fórmula geral:
Onde é a base, o nós chamamos de logaritmando ou de argumento da função logarítmica e o resultado é o logaritmo em si, que equivale sempre ao expoente em uma função exponencial.
Achando o na função
Imagine que tenhamos a função e queremos saber o valor de para qual . Igualando essas duas informações, temos:
Vamos transformar esse problema em um exponencial! Então a pergunta que faríamos para o logaritmo é: “A base elevada a qual número tem como resultado?" E como da igualdade acima sabemos que o resultado é , temos:
Isolando o ficamos com,
Lembrando que em divisão de exponenciais com a mesma base, a gente repete a base e substrai os expoentes!
Logarítmos Especiais
O logaritmo natural ou niperiano é o log de base , que é o número de Euler. O que você precisa saber dele agorá é que ele recebe uma notação especial de , podendo ser:
Dentre infinitas outras possibilidades.
Então se você vir um ln por aí, já fica sabendo que temos uma função logarítmica!
Além disso, quando a base da função logarítmica for , você não precisa escrever! Então:
E se você encontrar um logaritmo sem base, não precisa se desesperar! Lembra que tem um escondido ali!
Gráfico da função logarítmica
O gráfico da função logarítmica é um espelhamento do gráfico da função exponencial, como vemos abaixo no gráfico de , que é o gráfico da função espelhado em relação à linha tracejada:
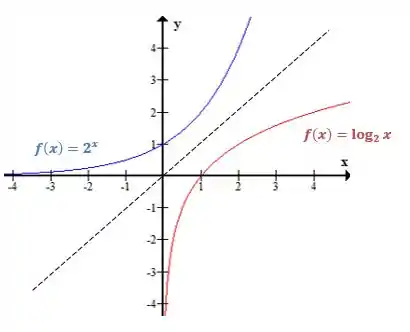
Podemos começar a análise do gráfico vendo que a curva toca o eixo quando , o que indica que o valor da função ali é igual a . Isso faz sentido, uma vez que:
Qual expoente leva qualquer número a ter como resultado ? !
Já que , para qualquer valor de .
Desse ponto, indo para a esquerda, vemos que conforme o se aproxima de zero, a função decresce cada vez mais.
Podemos entender, pensando nos exponenciais correspondentes, onde temos expoentes cada vez mais negativos, que resultam em valores cada vez mais próximos de zero, por exemplo:
E daí por diante!
Voltando ao , só que agora seguindo para a direita, vemos que quanto mais o valor de cresce, mais a função cresce.
Imagem e Domínio
Reparou que a curva que representa a função não está presente na região onde o possui valores negativos?
Isso acontece porque nossa base precisa sempre ser um número positivo e não dá para elevar um número positivo a alguma coisa e encontrar um resultado negativo disso. Então, restringimos o domínio da função logarítmica para valores positivos dentro do log.
Ou seja, para , nosso precisa ser sempre um valor real positivo, que escrevendo em matematiquês, fica:
Já para , novamente precisamos que os valores dentro do log sejam positivos, portanto:
O domínio dessa função será composto então pelos valores de reais e maiores que , que escrevendo mais uma vez em matematiquês, fica:
Já para a imagem da função, precisamos ver quais são os valores que temos como resultado da função, ou seja, vamos olhar pro .
Próximo ao vimos que a função decresce infinitamente e o pode assumir qualquer valor negativo, depois conforme o cresce, o também cresce infinitamente podendo assumir qualquer valor positivo. Então, não há limites pra imagem da função logarítmica, que pode assumir qualquer valor real:
E um detalhe importante é que a imagem não vai mudar mesmo que a gente tenha uma função daquelas diferentonas
Por hoje é só!