Funções Compostas e Funções definidas por Partes
Teoria
Este tipo é bem simples, você vai ver. Primeiro vamos ver o que é uma função composta e como utilizá-la. Depois vamos dar uma olhada nas operações básicas que podemos realizar com funções.
Função Composta
Bom, a primeira coisa que você precisa saber, pequeno gafanhoto, é que para termos uma função composta, precisamos de, pelo menos, duas funções. A função composta é então definida com uma função de função.
Ein?!
Não se assuste, vamos te explicar. Você tem um valor e uma função que associa ele a uma imagem :
E, depois, você tem uma outra função que associa o valor a uma imagem :
E não tem mistério, é só substituir o valor de ali dentro e...
Denotamos essa função composta “ de de ” por , como ilustrado acima, ou ainda, por
Não confunda com produto, a notação acima é lida “g de f de x” ou “g composta f”.
Note que a ordem da operação também é importante, já que:
E:
Dessa maneira, seja e , vamos calcular .
Note que para obter , primeiro tomamos e depois a aplicamos dentro de :
Agora basta substituir o em por , que é o argumento da função:
Partindo para outro exemplo, podemos também criar uma função composta aplicando outra diretamente no argumento da função. Como, por exemplo, para:
Se quisermos determinar , basta substituir por na expressão:
Funções definidas por partes
As funções definidas por partes ou funções chaveadas podem assustar um pouco para quem olha só o nome, mas em verdade não têm nada de mais. Vamos ver?
Essas funções são aquelas definidas por 2 ou mais expressões como no exemplo abaixo:
Isso significa que a função tem expressão:
Para todo , o que implica no gráfico:
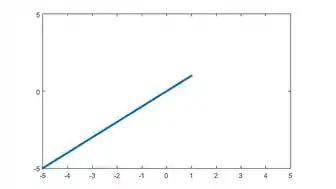
Que é o gráfico da reta , mas sim, parando em . Pois essa expressão só é válida para valores menores ou iguais a menos 1 ().
Para valores maiores que , a função assume a expressão:
Que juntando com o gráfico anterior, fica:
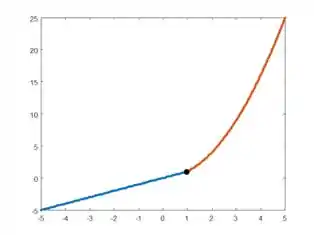
O gráfico em vermelho é o gráfico da parábola exibido a partir de .
Isso que fizemos é exatamente o que diz a expressão dada no início.
Não há a necessidade dos dois ou mais gráficos de uma função definida por partes estarem ligados, pode ocorrer um salto na interseção entre uma expressão e outra.
A função:
Tem o seguinte gráfico:
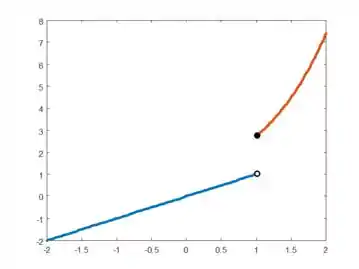
Repare que há um salto alí, as duas expressões não estão conectadas. Não há nenhum erro no esboço, muitas funções são assim mesmo. Falaremos da bolinha de recheio preto e a da bolinha de recheio branco na seção seguinte.
Esboço de funções definidas por partes
Por falar em esboço, esboçar uma função definida por partes em muito pouco se difere do esboço que vimos até agora. Para a função:
Podemos esboçar fazendo o esboço de cada expressão individualmente primeiro. Para , temos, por Bhaskara, as raízes:
Como o coeficiente do termo quadrático é maior que zero, a função é côncava para cima. Isso resultará no gráfico:
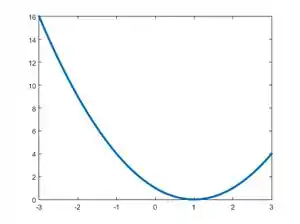
Agora, vamos para a segunda expressão, que é , uma linda reta, que corta o eixo em:
E o eixo em:
Gerando o gráfico (em vermelho):
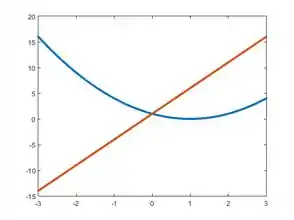
Com as duas curvas traçadas, podemos então limitar o gráfico de acordo com os intervalos de cada expressão. A parábola, é a expressão de para . Portanto, pontilhando os demais pontos:
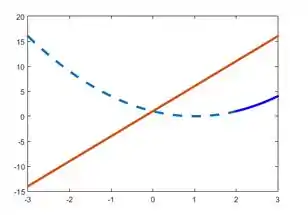
Seguindo o mesmo raciocínio para a reta:
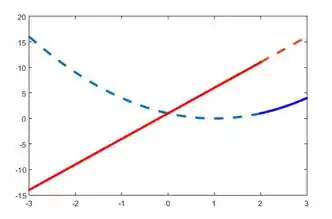
Agora, basta remover a parte pontilhada:
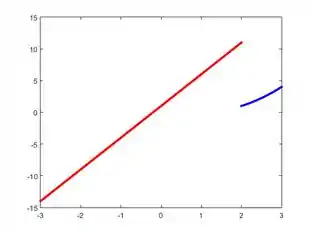
E praticamente teremos o nosso esboço. Falta só marcas as bolinhas de recheio branco e preto que citamos na seção anterior. A bolinha de recheio preto indica que aquele ponto faz parte da expressão da função. Como é válida para x (menor ou IGUAL), o ponto tem essa expressão e, portanto, marcamos com bolinha recheio preto.
De maneira análoga, a bolinha de recheio branco indica que aquele ponto não faz parte da expressão da função. Como é válida para (menor apenas), o ponto não tem essa expressão, portanto, marcamos com bolinha de recheio branco.
Isso resulta no esboço final:
\s
Então, o segredo é esboçar cada expressão como se fosse a única expressão da função e depois limitá-las ao intervalo da função chaveada.
Essas bolinhas são muito importantes quando estamos querendo determinar o domínio dessas funções. Por falar nisso:
Domínio e imagem de funções chaveadas.
Não há muito mistério quanto ao domínio de funções chaveadas. Será necessário verificar o domínio em cada uma das expressões e verificar se há restrições dentro do intervalo de cada expressão.
As funções vistas até agora, tinham todas expressões com retas, parábolas e exponenciais. Essas expressões têm sempre domínio nos números reais e, portanto, as respectivas funções definidas por partes também terão domínio:
Para outras expressões com restrições, como expressões com funções racionais, por exemplo, é necessário verificar se a restrição no domínio está dentro do intervalo proposto da região. A função:
Tem, na primeira expressão, um ponto de singularidade em , com todos os demais pontos pertencendo ao conjunto dos números reais.
Esse ponto, porém, não entra na restrição do domínio, pois essa expressão só é válida para , para , quem manda é a constante , que, em não tem nenhum problema.
Dessa maneira:
Porém, se os intervalos fossem:
O ponto teria como expressão a primeira, e portanto, deveria ser excluída a restrição no domínio:
Funções definidas por partes
Esboço de funções definidas por partes
Domínio e imagem de funções chaveadas.
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Dada as funções
Calcule a função composta
Passo 1
Primeiro devemos reconhecer a ordem das funções para obter a função composta:
Passo 2
Agora, substituindo no argumento de :
Resposta
Exercício Resolvido #2
UEPA 2014 (Adaptado)
Uma operadora de telefonia móvel oferece diferentes planos de ligações conforme a tabela a seguir:
Sabendo que essa operadora cobra R$ 0,50 por minuto excedente da franquia, independente do plano escolhido
- Construa o gráfico que melhor representa o valor a ser pago pelos clientes que optarem pelo plano A .
- Se uma pessoa pretende utilizar apenas 75 minutos da franquia, qual é o plano mais rentável?
Passo 1
Primeiro vamos entender como funciona essa plano, temos uma função entre os minutos utilizados (x) e o valor do plano (y).
Enquanto não chegamos no limite de minutos fornecidos pela franquia (50 minutos) , teremos a nossa função sendo dada por:
Para valores acima de 50 minutos, a função será dada por:
O gráfico vai ficar assim ó:
Passo 2
Agora vamos ver qual dos dois planos é mais vantagem para uma pessoa que irá usar somente 75 minutos.
Para o plano A, a pessoa irá pagar :
Ou seja, é mais vantagem utilizar o plano A do que o plano B, uma vez que no plano B a pessoa pagaria 55 reais.
Resposta
a)
b) Plano A
Exercício Resolvido #3
Elaboração Própria
Sejam as seguintes funções
E
Determine as seguintes funções
Passo 1
Aqui ele quer a soma das compostas e .
Vamos começar com , essa função na verdade vai ser
Vamos trocar pela fórmula dela
Isso quer fizer que a nossa função composta vai ser
Passo 2
Agora só falta . Podemos escrevê-la como
Trocando a pela sua equação vamos ter
Trocando isso na equação de vamos ter
Passo 3
Vamos agora para a soma das compostas
Arrumando isso vai ficar
Todos os coeficientes são pares, então podemos dividir geral por
Resposta
Exercício Resolvido #4
UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 2
Seja . Determine:
Passo 1
Não é tão difícil, conforme vimos na teoria, é só substituir pelo argumento sugerido. Para a letra (a):
E, para a outra, é a função normal ao quadrado e não o argumento ao quadrado como no primeiro caso.
Portanto:
Passo 2
Para a letra (b), seguimos o mesmo princípio:
E:
Assim:
Passo 3
Agora, na letra (c) é com argumento , ou seja:
Resposta
Exercício Resolvido #5
Elaboração Própria
Sejam as seguintes funções
E
Determine as seguintes funções compostas, e
Passo 1
Ele quer aquelas duas funções compostas, como vamos fazer isso? Primeiro vamos ver a primeira função , tá lembrado como faz isso?
Então preciso pegar a e “colocar dentro” da . Beleza, mas as funções são separadas em partes, e agora? Temos dois intervalo, certo? Então é só fazer a composta em cada pedaço do intervalo. Assim vamos ter a composta separada em intervalos também.
Vamos fazer a composta para e para e depois é só correr pro abraço!
Passo 2
Vamos começar fazendo a parte de , então vamos ter
Substituindo a fórmula de nesse intervalo, vamos ter
Trocando o valor de agora, vamos ter
E achamos a composta no primeiro pedaço.
Passo 3
Vamos agora para o outro intervalo,
Substituindo a fórmula de nesse intervalo, vamos ter
Trocando o valor de agora, vamos ter
Assim a nossa função composta vai ficar
Passo 4
Vamos agora fazer a outra função composta, . Essa função vai ser na verdade
De novo temos que fazer nos intervalos, vamos começar com , começando trocando o valor de
Trocando o valor de agora, vamos ter
Passo 5
Vamos agora para o outro intervalo,
Substituindo a fórmula de nesse intervalo, vamos ter
Trocando o valor de agora, vamos ter
Assim a nossa função composta vai ficar
E como falei, agora é só correr pro abraço!
