Introdução às funções
Teoria
Chegou a hora de falar de um dos assuntos mais importantes, a principal base que vamos precisar para finalmente aprendermos sobre o cálculo!
Sim, vamos falar de funções!!!!
Embora o assunto seja bastante extenso, pode ficar tranquilo! Não é um monstro que a gente não consegue domar rs
Vamos nessa?
O que são funções?
Para falar das nossas amigas funções, vamos começar com um pequeno exemplo. Imagine que você vai numa lanchonete comer hambúrgueres.
Se cada hambúrguer custa R$ 5,00, uma pergunta que você pode se fazer é: quanto você vai pagar em função da quantidade de hambúrgueres que você comer?
Para cada quantidade de hambúrgueres que você come, existe um preço correspondente. Se chamarmos a quantidade de hambúrgueres de , então, nós chamamos de o preço a pagar em função da quantidade de hambúrgueres.
Se você fosse comer um hambúrguer, quanto pagaria? Cinco reais? Usando essa notação que acabamos de falar vamos ter:
Perfeito? Ok, agora se você fosse comer dois hambúrgueres, você pagaria dez reais no total, né? De novo, usando a notação:
Repare que para achar o preço que vamos pagar, basta multiplicar a quantidade de hambúrgueres pelo preço de uma unidade. Isso nos diz que, para uma quantidade , o preço vai ser:
E esta é uma relação geral entre a quantidade e o preço, que nós chamamos de função.
Condição para função
Ok, vimos no exemplo, uma função, mas qual é a sua definição?
No nosso problema, temos duas variáveis: a quantidade hambúrgueres e o preço .
A quantidade de hambúrgueres é uma variável de valor arbitrário, pois não depende de nenhuma outra variável dentro do problema. Natural, afinal, João pode querer comer um hambúrguer. Maria, acabando com sua dieta, pode pedir dois e Pedro, que nunca ligou para nada mesmo, pode querer 3. Dessa forma, chamamos esse tipo de variável de variável independente.
Já o preço é sempre dependente da quantidade , afinal:
Ou seja, o quanto você vai pagar, DEPENDE de quantos hambúrgueres serão comprados.
Então, chamamos esse tipo de variável de variável dependente.
Para que tenhamos uma função, precisamos que o valor de , como o nome sugere, seja função do valor de , ou seja, precisamos que o valor de dependa do valor de .
Se o valor do preço depende da quantidade, então não podemos ter diferentes preços para uma mesma quantidade, certo? Então, para ser função, precisamos que só exista um valor de para cada valor de
A função é uma relação de dependência entre dois conjuntos, esses conjuntos não precisam ser numéricos...
Por exemplo, cada pessoa possui um único tipo sanguíneo, sendo assim, podemos pensar em uma função que liga um conjunto de pessoas e associa a elas o seu tipo sanguíneo
Perceba que a gente sempre RELACIONA um conjunto ao outro e um depende do outro. Nesse caso, as pessoas dependem de um tipo sanguíneo, mas não o contrário.
Podemos pensar em uma relação de pessoas com o seu time favorito, no entanto, uma mesma pessoa pode ter mais de um time favorito, ou seja, essa relação NÃO vai ser uma função!!!
Para ser uma função, para cada valor de x existe somente um único valor de y associado.
No caso da relação entre as pessoas e os times de futebol, uma pessoa pode torcer para o Flamengo e para o Real Madrid, por exemplo. Teríamos então algo assim:
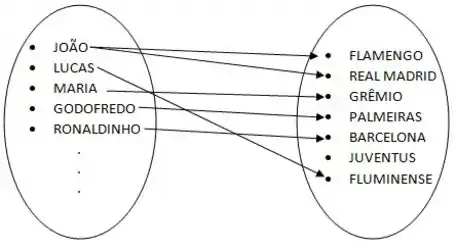
Esse é um exemplo de uma relação que não é uma função. Para que fosse uma função, cada pessoa só poderia ter um único time.
Embora esses exemplos sejam legais para entendermos o conceito de função, normalmente o que você verá, serão contas.
Vamos definir o que é uma função?
Dada uma variável independente e uma variável dependente , dizemos que é função de
se e somente se para cada valor de , existir somente um único valor de associado.
É necessário registrar que essa definição é coerente com a ideia de funções de uma única variável, que serão aquelas que você vai precisar se preocupar por hora.
Maneiras de representar uma função
Um grande herói tem muitas faces e não poderia ser diferente com as funções. Existem várias maneiras de representar uma mesma função. Ainda falando de hambúrgueres, vimos que:
Essa é a forma algébrica da função. Assim como, para outras funções, temos:
Ela surge quando temos uma fórmula matemática para achar o valor da função para um dado valor de sua variável independente.
Quando queremos ter uma visão geral do comportamento da função com a variação da sua variável independente, é mais interessante traçar um gráfico, ou seja, representar graficamente a função. Para a função , por exemplo:
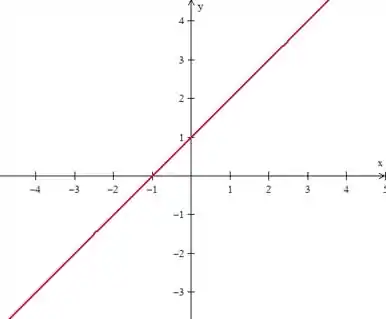
Neste caso, temos que a função é uma reta no gráfico. Isso nem sempre é verdade, como quando na parábola:
Onde:
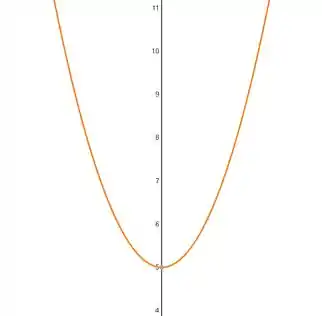
Além disso, também podemos descrever a função verbalmente, como encontraremos no enunciado de vários exercícios:
“Uma fábrica tem produção de 57 sapatos por hora ”
“Um objeto é solto e cai livremente a partir de uma posição inicial de referência zero.”
Existem outras maneiras de representar uma função, mas vamos parar por aqui para evitar a fadiga.
Domínio
Agora chegamos numa parte que é muito cobrada em prova e muitos acabam se confundindo. Isso não vai acontecer com você. Dê-me a mão e vamos juntos mais uma vez.
Hambúrgueres são de fato muito gostosos, então vamos usar o exemplo deles novamente. O atendente da lanchonete dificilmente vai te vender meio hambúrguer. Você pode até dividir com seu colega, mas certamente a quantidade de hambúrgueres comprada será sempre inteira.
Da mesma maneira, não dá para ter uma quantidade negativa de hambúrguer, então é sempre maior ou igual a zero e inteiro
Podemos dizer, então, que pertence ao conjunto dos números naturais, ou:
Esse é conjunto de todos os valores possíveis para , que é a variável independente do nosso sistema. O conjunto de valores possíveis para a variável independente de uma função é justamente o domínio da função. Portanto, poderíamos escrever também:
Agora vamos a outro exemplo: Imagine que a função fosse a posição , em quilômetros, de um carro em função do tempo , em horas. Poderíamos ter valores fracionados para o tempo, como horas. Quanto ao sinal, não teremos tempo negativo, certo?
Logo, o domínio seria o conjunto de todos os números maiores ou iguais a zero, inteiros ou não, ou seja:
Onde o subscrito indica que o conjunto está restrito aos seus valores não-negativos.
O domínio vai depender do que a nossa lei de formação está tratando, existem infinitas formas de representarmos nosso domínio.
Restrições no domínio
Algumas funções, como as funções polinomiais, que são aquelas com somas de potências naturais de com coeficientes constantes como:
Não possuem qualquer restrição ao domínio, o que significa que seu domínio será sempre o conjunto dos números reais.
Já para outras funções, o domínio nem sempre vai ser um conjunto completo, muitas vezes, a variável independente não poderá assumir alguns valores específicos. Quais seriam esses valores?
Lá atrás, muito provavelmente você ouviu sua professora falar que não podia dividir nada por zero. O mesmo vale para funções. Pontos em que ocorre a divisão por zero não pertencem ao domínio, pois geram indeterminações ou singularidades.
Da mesma maneira, como o nosso estudo estará sempre restrito aos números reais e a seus subconjuntos, não poderemos ter também raiz quadrada de número negativo, pois isso gera números complexos que estão fora do nosso papo por enquanto. Logo, pontos onde aparece raiz quadrada negativa não pertencem ao domínio. Ou seja, você precisa ficar atento para:
Funções racionais (funções representadas por divisão de polinômios): valores para os quais o denominador zera, não pertencem ao domínio. Como em:
Ou seja,
Em , temos que a função está divida por zero, então esse ponto não faz parte do domínio, que será o conjunto dos reais sem o .
Funções com raiz quadrada: valores para os quais a raiz é negativa, não pertencem ao domínio. Como em:
Então pense:
Todos os valores de menores que levam a valores negativos dentro da raiz, logo:
Existem outras restrições para o domínio de outros tipos de funções, mas falaremos delas na teoria correspondente.
Contradomínio
Enquanto o domínio está relacionado com a variável independente, o contradomínio se relaciona com a variável dependente. Trata-se de todos os valores que a última pode assumir.
Dentro do exemplo do carro, pode assumir vários valores: pode ser positiva quando depois do referencial da posição, zero quando sobre o referencial e negativa quando antes.
A variável também pode ser não inteira, afinal, o carro não dará saltos de quilometro em quilômetro (Já pensou que louco seria? hahahaha).
Assim, o contradomínio para o nosso exemplo, será igual os números reais sem restrição:
Imagem
Você pode se confundir quanto à diferença entre contradomínio e imagem, pois ambos se referem a variável dependente. Porém, enquanto o contradomínio indica todos os valores que a variável dependente pode assumir, a imagem trata de todos os valores que ela irá assumir. Querer não é poder, jovem.
Por exemplo, pense no salário mensal de um vendedor que tem uma parte fixa de R$ 1000 reais e mais 1% de comissão em cima do quanto conseguiu vender. Nossa função será:
Onde:
Sabemos que esse vendedor em hipótese nenhuma poderá ganhar menos do que 1000 reais, mesmo que ele não faça nenhuma venda durante o mês!!!
Isso significa que a imagem, ou seja, os valores possíveis para o seu salário serão:
Leia-se: pertencente () ao conjunto dos números reais (), tal que seja maior ou igual a 1000.
Maneiras de representar uma função
Domínio
Restrições no domínio
Contradomínio
Imagem
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Represente por diagrama de flechas e verifique se são funções de cada relação abaixo:
a) , sendo
b) sendo
Passo 1
Show o que a gente precisa observar é que para ser uma função TODO elemento do Domínio (Conjunto A nesse caso) precisa se relacionar a UM ÚNICO elemento do CONTRADOMÍNIO (Conjunto B nesse caso).
Então, o que vamos fazer é colocar os elementos de A na nossa lei de formação e ver o que acontece.
Por exemplo,
Para teremos
Para teremos
Para teremos
E assim por diante...
Depois é só a gente relacionar os valores de um conjunto com o do outro e encontraremos algo assim:
Agora vamos observar duas coisas:
- Se todo elemento do domínio está se relacionando com alguém
- Se os elementos do domínio estão relacionados a um único elemento do contradomínio
Essas duas condições estão sendo satisfeitas, logo é uma função de A em B =D
Passo 2
Vamos repetir o processo para a letra b)
Temos agora a seguinte lei de formação:
Esses são os valores que x pode assumir:
Para teremos
Para teremos
Para teremos
E assim por diante...
Montando os dois conjuntos e os relacionando, teremos:
Opa, espera um pouco, percebeu que o não está relacionado com ninguém? Observa só:
Para teremos
Se tivermos temos uma indeterminação.
Logo, não vai atingir nenhum elemento de B, sendo assim NÃO será uma função. Pois nem todo elemento do Domínio está relacionado a um elemento do contradomínio.
Resposta
- É uma função.
- Não é função.
Exercício Resolvido #2
Elaboração própria
Observe o gráfico abaixo e determine os conjuntos domínio e imagem.
Passo 1
Beleza, primeiro vamos determinar o domínio dessa função, serão todos os valores possíveis para o x.
Se você observar bem, verá que a função está definida para qualquer valor de x que estiver entre -2 e 5.
Agora é só escrevermos isso mais bonitinho, fica assim, ó:
Passo 2
Vamos partir para a imagem agora :D
A imagem será dada por todos os valores que o x irá atingir no y.
Observe que no intervalo a função atinge os seguintes valores em y
Ou seja: O y precisa ser maior ou igual a -4 e menor que 0
Só atenta a uma coisa importante, quando temos aquela “bolinha fechada” em um ponto, isso significa que estamos incluindo ele, da mesma forma que um ponto com a “bolinha aberta” está excluindo ele da função. Na hora de escrevermos, em termos práticos, se tiver com a bolinha fechada, você inclui o ponto colocando o igual junto ao sinal de desigualdade, caso contrário, você não põe nada. Beleza?
Vamos aos próximos intervalos...
Para
E por último...
Para
Escrevendo isso de uma forma mais elegante, temos:
Resposta
Exercício Resolvido #3
MVP UFF - Assunto 1 - E_20
Determine o domínio da seguinte função:
Passo 1
Para acharmos o domínio dessa função precisamos ver as restrições que ela tem. Repara que tem raiz quadradas ali né? Então queremos que o cara dentro de cada uma delas seja maior ou igual a . Além disso, temos uma expressão no denominador, neste caso queremos que ela seja diferente de .
Então para entender melhor as restrições, vamos primeiro analisar a parte e depois a parte .
Passo 2
Vamos começar com a parte,
E como mencionamos no Passo 1, o denominador não pode zerar. Com isso temos que,
Também foi comentado que dentro de cada raiz tem ser um valor maior ou igual a . Em outras palavras, nós temos essa restrição,
Mas do jeito que ela está escrita, está difícil de analisar quando ela vai respeitar essa condição. Então vamos dar uma arrumada nela para entender melhor. Para isso vamos aplicar um produto notável ali em cima,
Com isso, achamos duas restrições:
Agora vamos guarda essa informação, pois no fim vamos relembrar essas restrições para a resposta final.
Passo 3
Vamos para outra parte da função,
Seguimos com a restrição para raiz quadrada, ou seja, dentro dela tem que ser um valor maior ou igual a . Com isso temos que,
Para resolver essa parte, temos que fazer o gráfico e olhar como fica o sinal. Para fazer o gráfico precisamos:
- Achar as raízes dessa função
- Achar a concavidade dessa função
Vamos começar achando as raízes,
Assim vamos ter
Passo 4
Agora vamos para o segundo passo, que é achar a concavidade dessa função, repara que temos
Assim, como , essa função é côncava para cima
Passo 5
Beleza, agora que sabemos essas duas informações podemos fazer o esboço do gráfico. Quando fizemos gráfico antes nós completávamos o gráfico com os outros dois pontos importantes, mas como aqui só queremos ver o sinal, não vamos achar esses pontos porque são contas a mais.
O esboço do gráfico vai ficar
Podemos perceber então que entre as raízes ( e ), ele vai ser negativo, e na outra parte vai ser positivo, vamos deixar isso um pouco mais claro
Beleza, achamos os sinais, agora vamos ver qual ele pede. Ele quer que essa função seja positiva para poder ter a raiz quadrada, assim, para essa parte precisamos ter
Passo 6
Pronto, chegou a hora de juntar todas as restrições que achamos!
Da primeira parte temos:
Da segunda parte temos:
Queremos que ele obedeça todas as condições! Repara que eu dei uma letrinha para cada restrição para facilitar nossa análise.
Vamos começar juntando e . Pois elas delimitam um intervalo que está inserido . Então podemos escrever assim,
Mas perai, olhando restrição , vemos que não pode ser e ele tá nesse intervalo. Então vamos dividir ele assim,
Repara que não colocamos o sinal igual para o Ele só pode ser menor ou maior que esse valor.
Por fim, vamos olhar para nossa restrição . Então, ela vai ficar como se fosse um buraco entre e no nosso domínio. Olha essa figura abaixo,
Escrevendo bonitinho matematicamente, ficamos com,
Resposta
Exercício Resolvido #4
UFF, Cálculo IA-Lista 1, GMA, 2008-1, 23
Abaixo, a função real de variável real é definida por sua expressão analítica. Determine o seu domínio.
Passo 1
Precisamos que a parte dentro da raiz seja sempre positiva. Vamos começar com a raiz mais interna:
Bem, essa não é difícil. Veja que temos subtraído de um valor ao quadrado. Essa diferença será negativa quando , ou seja, para ou .
Dessa maneira, tem que estar no intervalo:
Passo 2
Certo, agora vamos olhar para dentro da outra raiz. Temos:
E precisamos que isso seja sempre positivo. Para tal:
Mas, como vimos no passo anterior, é subtraído de um valor ao quadrado. Ou seja, o valor máximo da expressão será sempre menor ou igual a .
Com isso, garantimos que:
É sempre positiva para todo . Com isso, a nossa única restrição ao domínio será aquela que achamos no passo mesmo.
Resposta
Exercício Resolvido #5
Elaboração própria.
Determine o domínio da função abaixo
Passo 1
Nossa função está assim, ó:
Pra essas expressões vamos ter duas restrições aqui:
Para que a raiz do denominador seja um número real, a função dentro dela tem que ser maior ou igual a zero!
Essa restrição diz que tem que ser maior que zero, pois está no denominador! Então nesse caso não pode nem ser igual a zero, beleza?
Passo 2
Comparando as duas restrições a gente vê que é mais restritiva que . Isso significa que nem todos os valores para são válidos pra satisfazer a condição do nosso denominador ser positivo, então a restrição que vai prevalecer vai ser então:
E esse vai ser o domínio de .