Série de Potência
Teoria
O que é uma Série de Potência?
Uma série de potência nada mais é do que um polinômio escrito na forma de um somatório. Por exemplo:
O detalhe das séries de potência é que o polinômio nunca tem fim, ou seja, a gente pode continuar escrevendo parcelas até o infinito. Então, uma série de potência é uma série de polinômios, ou seja, funções com infinitas parcelas e com diferentes potências que variam junto com seus coeficientes. Um somatório infinito de parcelas, que cresce variando o expoente da potência do
Aqui temos uma série de potência com infinitas parcelas, onde chamamos
Por exemplo, se
E se eu dissesse para você que
Legal, né?! Séries de potência são apenas polinômios infinitos.
Definição geral de Série de Potência
As séries de potência que vimos acima são apenas exemplos. A forma geral de uma série de potência é:
EITA! Quanto símbolo! Mas aqui no RespondeAí a gente analisa isso tudo com calma.
A gente já conhece o
Então se eu te dissesse, por exemplo, que
Que é exatamente o exemplo que vimos acima.
Um outro exemplo, seria um série centrada em
E assim por diante!
Então, vamos olhar de novo a definição da série de potência:
Então podemos dizer que:
: é o índice da série : representa os coeficientes do polinômio : é a variável : é o centro da série
Representação em série de potência
TA, MAS PARA QUE EU PRECISO APRENDER SÉRIES DE POTÊNCIA?
As séries de potência são importantes, porque somos capazes de utilizá-las para replicar funções em determinados intervalos do eixo
Por exemplo, a representação em série de potência da função seno centrada em
Eu sei que parece algo impossível de entender, mas chegaremos lá com calma.
Agora que temos uma série de potência, a gente pode expandir ela para qualquer valor de
Olha essa imagem que linda:
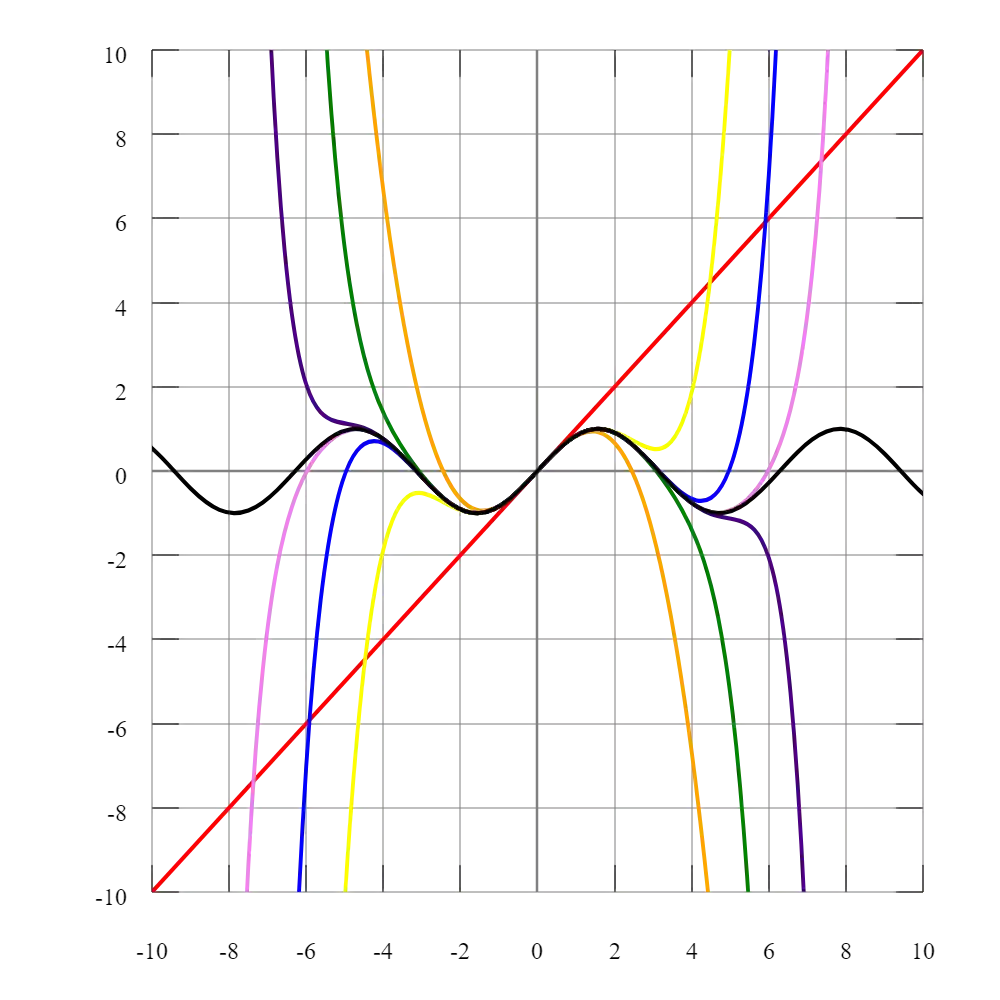
Nessa figura temos as aproximações da função seno utilizando a série de potências acima, com diferente número de parcelas, a legenda seria:
- Em vermelho, aproximação com 1 parcela
- Em laranja, aproximação com 3 parcelas
- Em amarelo, aproximação com 5 parcelas
- Em verde, aproximação com 7 parcelas
- Em azul, aproximação com 9 parcelas
- Em roxo, aproximação com 11 parcelas
- Em rosa, aproximação com 13 parcelas
- E em preto, a verdadeira função Seno
Repara que quanto mais aumentamos o número de parcelas, maior é o intervalo que nossa série de potência consegue representar da função seno. Teoricamente com infinitas parcelas, conseguiríamos representar toda a função, ou teríamos que descobrir o raio de convergência e o intervalo de convergência daquela série.
Ou seja para conseguirmos fazer tudo isso que estou lhe propondo, precisamos sempre estudar se a série é convergente ou divergente. E é por isso que estamos aqui.
Muita coisa legal né? Se você assinar nosso conteúdo vai encontrar um assunto com tudo que você precisa saber sobre série de potências, com exercícios resolvidos e conteúdos em vídeo e tudo para você mandar bem nas suas provas de Cálculo.
Exercícios
Aproveita e confere um de nossos vídeos de exercício do nosso tópico de Introdução à Série de Potência:
Encontra uma representação em série de potências para a função:
Definição geral de Série de Potência
Representação em série de potência
Exercícios
Exercícios Resolvidos
Exercício Resolvido #1
PUC-RJ - Cálculo 3 - P3 2014.2 - 3
Ache a expansão em série de potências de em torno de
Passo 1
Bom, primeiro vamos reescrever de maneira esperta!
Passo 2
Veja então que tem a cara da função:
Com .
Que é exatamente a fórmula do valor da série geométrica de razão e primeiro termo igual a .
Passo 3
Então, temos que
Resposta
Exercício Resolvido #2
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, São Paulo: CENGAGE learning, 2010, pp. 697, 9(adaptado)
Encontre uma representação em série de potências para a função
Passo 1
Para representar a função em séries de potências é bom tentar comparar a função com a série geométrica!
Então é bom escrever a função de forma que apareça um termo semelhante a:
Logo, vamos ver se conseguimos escrever de outra forma!
Que pode ser rescrito como
Passo 2
O segundo cara entre parênteses é a série geométrica, certo?
De forma que a gente fica com
Passo 3
Expandindo isso ficamos com
Beleza! Mas dá pra simplificar mais um pouco! É só lembrar que
E
De forma que , , , , vão aparecer duas vezes no nosso e o vai aparecer só uma vez! Assim
Resposta
Exercício Resolvido #3
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, São Paulo: CENGAGE learning, 2010, pp. 697, 10(adaptado)
Encontre uma representação em série de potências para a função
Passo 1
Para representar a função em séries de potências é bom tentar comparar a função com a série geométrica!
Então é bom escrever a função de forma que apareça um termo semelhante a:
Logo, vamos ver se conseguimos escrever de outra forma!
Para , podemos dividir o numerador e o denominador por :
Continuamos não tendo nada que seja legal de ser comparado com a série geométrica... Então vamos fazer o seguinte,
Agora vamos escrever a fração como série de potências e multiplicar por , ficou bem mais fácil!
Passo 2
Comparando com a série geométrica, teremos
Passo 3
Por fim, vamos multiplicar por ,
Resposta
Exercício Resolvido #4
PUC-RJ - Cálculo 3 - P3 2013.1 - 4(adaptado)
Calcule o termo geral da expansão em série de potências de da função abaixo
Passo 1
Se queremos escrever o termo geral em série de potências de , precisamos que apareça esse termo na nossa função. Então vamos começar escrevendo que:
E então veja que se escrevermos:
E resolvendo o sistema:
Encontramos: e .
Reescreveremos a função assim:
Passo 2
Como queremos que apareça o termo , vamos escrever que:
E agora repare que podemos escrever essa função como o valor da série geométrica, cuja razão será descoberta a seguir.
Colocando o em evidencia, podemos escrever a serie a assim:
Vamos fazer a mesma coisa pro :
E esses termos da forma:
São exatamente a fórmula do valor da série geométrica de razão e primeiro termo igual a . Portanto, podemos escrever que:
Passo 3
E agora voltando pra expressão de :
Agora vamos escrever a série juntando dos somatórios encontrados no passo anterior,
E colocando o termo que queremos em evidência: