Considere o sistema com realimentação unitária da figura abaixo com
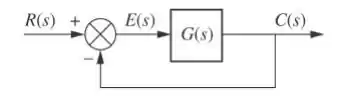
Utilizando o critério de Routh-Hurwitz, determine a região do plano onde os polos do
sistema em malha fechada estão localizados.
Passo 1
Para aplicar o método de Routh-Hurwitz, precisamos definir a equação característica do sistema, e para encontrar a equação característica, precisamos da função de transferência em malha fechada para o sistema.
Utilizando álgebra de diagrama de blocos, teremos:
Substituindo:
Manipulando a expressão encontrada:
A equação característica do sistema é sempre o denominador da função de transferência em malha fechada. Portanto, a nossa equação característica será:
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
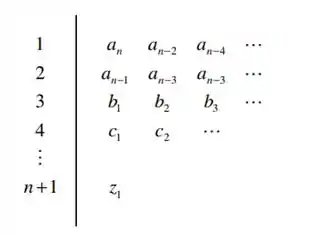
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
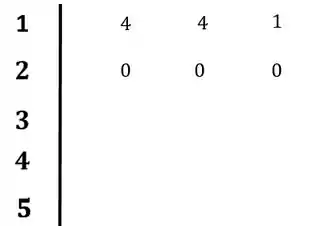
Logo de cara já encontramos uma linha de zeros na segunda linha. Precisaremos então usar o nosso polinômio auxiliar para encontrar novos valores para a nossa linha.
Nesse caso, o polinômio auxiliar terá o mesmo grau da primeira linha, ou sea, quatro, e coincidentemente será igual à nossa equação característica:
Derivando o polinômio auxiliar:
Com os coeficientes desse novo polinômio, podemos substituir a linha de zeros que tínhamos encontrado antes:
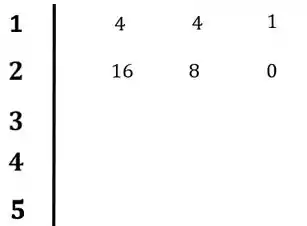
Passo 3
Para a terceira linha teremos:
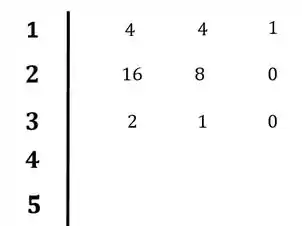
E a quarta linha:
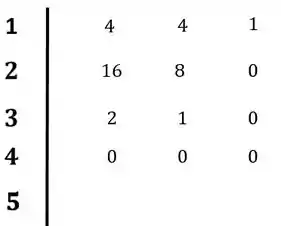
Passo 4
Inferno! Mais uma vez uma linha de zeros, vamos lá novamente, polinômio auxiliar:
Derivando o polinômio auxiliar:
Substituindo a linha de zeros:

Terminando de preencher o diagrama teremos:

Passo 5
Falta agora responder onde estão os polos desse sistema em malha fechada.
Bom, uma coisa que podemos reparar logo de cara é que nosso primeiro polinômio auxiliar teve grau quatro, o que significa que existem 4 polos simétricos no nosso sistema, como 4 também é o grau da equação característica, podemos dizer que todos os polos do sistema em malha fechada são simétricos.
Além disso, não tivemos nenhuma mudança de sinal, o que indica que não temos nenhum polo no semiplano direito. Sendo assim, como todos os polos são simétricos e não temos nenhum polo no lado direito, podemos concluir que todos os polos do sistema estão sobre o eixo .
Resposta
Todos os quatro polos estão sobre o eixo .