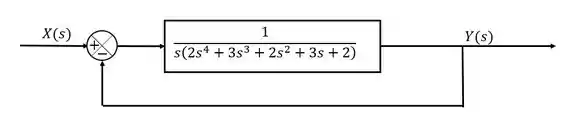
Determine o número de polos no semiplano da esquerda e no semiplano da da direita para o sistema da figura abaixo:
Passo 1
Primeiramente, devemos determinar qual é a nossa função de transferência em malha fechada para conseguir a equação característica do sistema.
Usando álgebra de diagrama de blocos teremos:
A equação característica do sistema é sempre o denominador da função de transferência em malha fechada. Portanto, a nossa equação característica será:
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
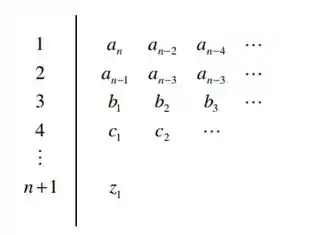
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:

Passo 3
Vamos agora calcular os coeficientes da terceira linha conforme as expressões abaixo:
Colocando os valores no diagrama:
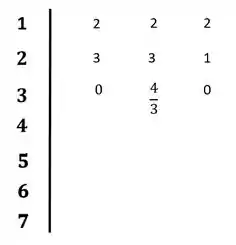
Temos aqui um na primeira coluna, o que é um problema, vamos então utilizar o método do épsilon, substituir nosso zero, e continuar daí:
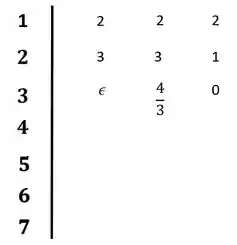
Passo 4
Continuando montando o diagrama a partir daí, teremos:
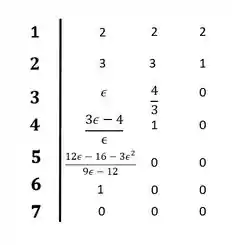
Para determinar a estabilidade precisamos ver o que acontece quando épsilon assume valores muito pequenos.
Por exemplo, se épsilon for um número positivo muito pequeno, o termo da primeira coluna da linha cinco assumirá um valor negativo, enquanto o termo da primeira coluna será positivo, tendo assim duas trocas de sinais na primeira coluna: da linha três para a linha quatro, e da linha quatro para a linha cinco.
Da mesma forma, se épsilon for um número negativo muito pequeno, teremos o termo da primeira coluna na linha três negativo, na linha quatro positivo, e na linha cinco positivo, tendo novamente duas trocas de sinais.
Portanto, o sistema é instável e apresenta duas raízes no semiplano direito, pois a primeira coluna do diagrama de Routh-Hurwitz mostra duas trocas de sinais.
Resposta

Duas raízes no semiplano direito e três no semiplano esquerdo.