Quantos polos estão no semiplano da direita, no semiplano da esquerda e sobre o eixo para o sistema em malha fechada abaixo:
Passo 1
Para aplicar o método de Routh-Hurwitz, precisamos definir a equação característica do sistema. A equação característica do sistema é sempre o denominador da função de transferência em malha fechada. Como a função de transferência já foi dada, a nossa equação característica será:
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
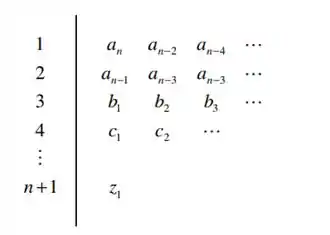
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
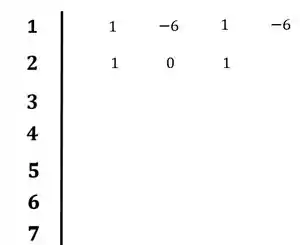
Passo 3
Para a terceira linha teremos:
Adicionando a nova linha:

E a quarta linha:
Colocando a quarta linha:

Passo 4
Caímos no caso da linha só de zeros. Vamos então determinar nosso polinômio auxiliar a partir da linha anterior:
Derivando o polinômio:
Podemos agora substituir o coeficientes obtidos no lugar da linha de zeros:

Passo 5
Vamos para a quinta linha agora:

Putz, agora ainda fomos abençoados com um zero na primeira coluna. Vamos ter que usar o método do épsilon:

Famos finalizar agora calculando tudo em função de épsilon:

Passo 6
Vamos fazer a nossa análise então. Primeiramente, vamos ver quantas mudanças de sinal existem na primeira coluna. Se épsilon for positivo teremos uma mudança de sinal da segunda para a terceira linha, da quarta para quinta e da quinta para sexta. Três mudanças de sinais.
Se épsilon for negativo, teremos mudança de sinal da segunda para a terceira linha, da quinta para a sexta e da sexta para a sétima. Novamente três mudanças de sinal.
Sendo assim, temos três polos no lado direito. Mas e os outros três polos, estão do lado esquerdo ou sobre o eixo ?
O nosso polinômio auxilizar apareceu na linha quatro e tinha grau quatro também. Sendo assim temos quatro polos simétricos e dois assimétricos. Uma mudança de sinal aconteceu antes da linha de zero aparecer, portanto entre os assimétricos um polo está no lado esquerdo e um no lado direito.
Após a linha de zeros, tivemos duas mudanças de sinais, o que indica que dois dos polos simétricos estão do lado direito, sendo assim, para que esses polos tenham simetria em relação à origem, é preciso que os outros polos apareçam do lado esquerdo. Sendo assim, não temos nenhum polo sobre o eixo .
Resposta
Três polos do lado direito e três polos do lado esquerdo.