Dado o sistema em malha fechada
Determine a estabilidade deste sistema pelo método de Routh-Hurwitz.
Passo 1
Para aplicar o método de Routh-Hurwitz, precisamos definir a equação característica do sistema.
A equação característica do sistema é sempre o denominador da função de transferência em malha fechada. Portanto, a nossa equação característica será:
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
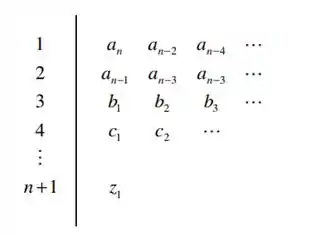
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
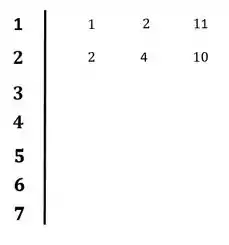
Passo 3
Vamos agora calcular os coeficientes da terceira linha conforme as expressões abaixo:
Colocando os valores no diagrama:
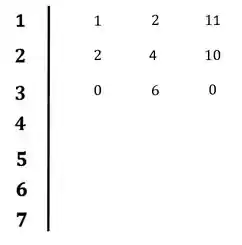
Opa! Caímos naquele caso onde temos um zero na primeira coluna. Não é legal quando acontece isso porque se não fizermos nada na próxima linha teremos uma divisão por zero que vai travar todo o nosso diagrama, sendo assim, uma solução rápida para driblar esse problema é substituir o zero por épsilon.
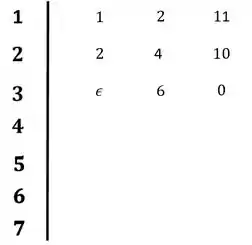
Passo 4
Vamos então continuar calculando o nosso diagrama a partir daí. Sempre que épsilon aparecer, a gente deixa o valor em função de épsilon.
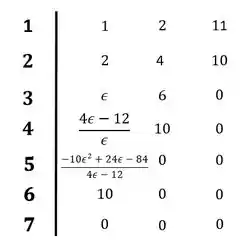
Para determinar a estabilidade precisamos ver o que acontece quando épsilon assume valores muito pequenos.
Se épsilon for muito pequeno e positivo, o valor da primeira coluna na terceira linha será positivo, na quarta linha, porém, será negativo, e na quinta linha ele volta a ser positivo, tendo portanto duas trocas de sinais.
Se ele for negativo, o valor da terceira linha será negativo, e os valores da quarta e da quinta linha serão positivos. Teremos novamente duas trocas de sinais.
Portanto, o sistema é instável e existem duas raízes da equação característica no semiplano direito.
Resposta
Sistema instável