Utilizando a tabela de Routh, diga quantos polos da função a seguir estão no semiplano da
direita, no semiplano da esquerda e sobre o eixo :
Passo 1
Para determinar quantas raízes estarão no semiplano da direita, podemos utilizar o método de Routh-Hurwitz. O número de mudanças de sinal na primeira coluna do diagrama corresponderá ao número de raízes no semiplano direito.
O exercício já nos deu a função de transferência em malha fechada. Para aplicar o método de Routh-Hurwitz precisamos da equação característica, que nada mais é do que o denominador dessa função:
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
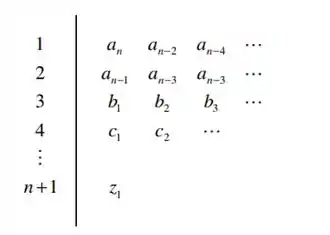
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
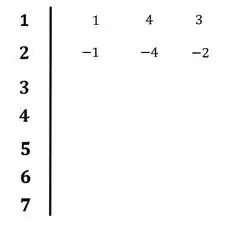
Passo 3
Vamos preencher a linha três seguindo as correlações de Routh-Hurwitz:
Colocando a nova linha no diagrama:
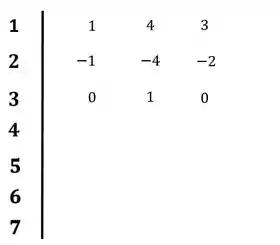
Demos de cara com um problema, que é a presença de um zero na primeira linha. Para contornar esse problema, vamos substituir esse zero po um épsilon e seguir nossa vida como se nada tivesse acontecido:
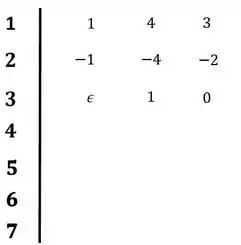
Passo 4
Seguindo a montagem do diagrama teremos:

Para determinar a estabilidade precisamos ver o que acontece quando épsilon assume valores muito pequenos.
Se o épsilon for um número muito pequeno positivo o número da primeiro coluna da linha três será positivo, da linha quatro também será positivo, e o mesmo acontecerá na linha cinco. A primeira coluna teria portanto três trocas de sinais: da primeira para a segunda linha, da segunda para a terceira e da quinta para a sexta.
Da mesma forma, se épsilon for um número negativo muito pequeno, teremos o termo da primeira coluna na linha três negativo, e nas linhas quatro e cinco positivo, que resultaria em três trocas de sinais novamente: da linha um para a dois, da três para a quatro e da cinco para a seis.
Portanto, temos três polos no semiplano direito e dois no semiplano esquerdo.
Resposta

Três raízes no semiplano direito e duas no semiplano esquerdo.