A função de transferência em malha fechada de um sistema é
Determine quantos polos em malha fechada estão no semiplano da direita, no semiplano da
esquerda e sobre o eixo .
Passo 1
Para aplicar o método de Routh-Hurwitz, precisamos definir a equação característica do sistema.
A equação característica do sistema é sempre o denominador da função de transferência em malha fechada. Portanto, a nossa equação característica será:
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
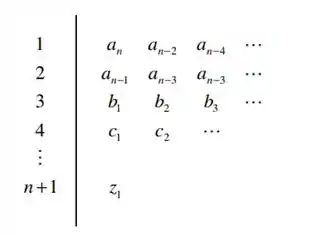
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
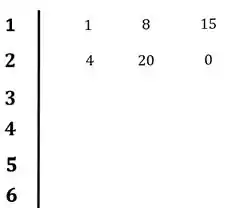
Passo 3
Vamos agora calcular os coeficientes da terceira linha conforme as expressões abaixo:
Colocando os valores no diagrama:

Passo 4
Prosseguindo para a quarta linha:
Colocando no diagrama:
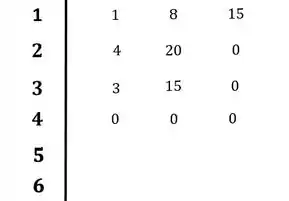
Bom, caímos numa linha de zeros. Sendo assim, precisamos do nosso polinômio auxiliar que pegaremos da linha de cima. A linha de cima é a terceira linha, como a primeira tem ordem quatro, a segunda terá ordem três e a terceira, ordem dois. Portanto o nosso polinômio auxiliar será:
Agora devemos derivar o polinômio para obter os valores que colocaremos no diagrama:
Colocando no diagrama:

Passo 5
Prosseguinto o restante da montagem do diagrama agora:
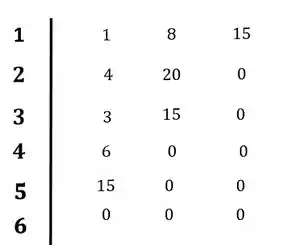
Não temos nenhuma troca de sinais na primeira coluna, o que indica que não existem raízes no semiplano direito.
Além disso, o nosso polinômio auxiliar apresentou ordem 2, o que significa que existem duas raízes simétrica em relação à origem. Como essas raízes não estão no semiplano direito, a única forma de elas serem simétricas é estando sobre o eixo .
Portanto, temos duas raízes no semiplano esquerdo e duas raízes sobre o eixo .
Resposta
Duas raízes no semiplano esquerdo e duas raízes sobre o eixo .