Determine quantas raízes no semiplano direito possui o polinômio abaixo:
Passo 1
Para saber quantas raízes do polinômio serão poxitivas (semiplano direito) podemos usar o critério de Roth-Hurwitz. A quantidade de troca de sinais que ocorrerem na primeira coluna do diagrama corresponderá ao número de raízes no semiplano direito.
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
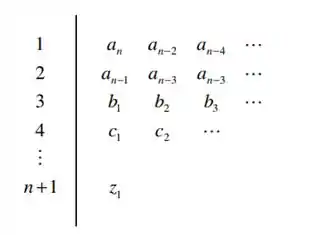
Passo 2
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
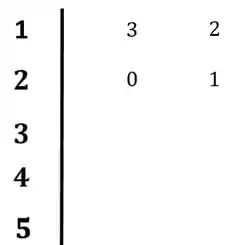
Logo de cara vemos que algo de errado não está certo. Esse zero na primeira coluna vai complicar a nossa vida, para lidar com ele a gente substitui o zero por épsilon, e segue a partir daí:
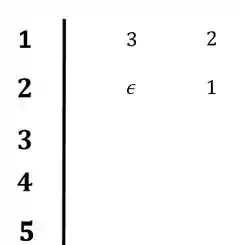
Passo 3
Vamos preencher a linha três seguindo as correlações de Routh-Hurwitz:
Colocando a nova linha no diagrama:
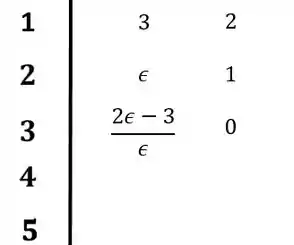
E prosseguindo a montagem:
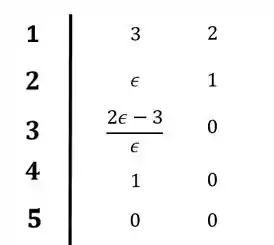
Passo 4
Vamos fazer a análise do nosso diagrama agora. Para isso precisamos imaginar que épsilon é um número muito pequeno, positivo ou negativo, e ver o que acontece com os sinais dos números da primeira coluna.
Se épsilon for um número positivo muito pequeno, nós teremos que o número na primeira coluna da segunda linha será positivo, e da terceira linha será negativo. Sendo assim, ocorrerão duas trocas de sinais, da segunda para a terceira linha e da terceira para a quarta.
Agora se épsilon for um número pequeno negativo, nós teremos o número da primeira coluna na segunda linha negativo e na terceira linha positivo. Portanto, acontecerão também duas trocas de sinais: da primeira para a segunda linha e da segunda para a terceira.
Então chegamos à conclusão que existem duas raízes positivas do polinômia porque temos duas trocas de sinais na primeira coluna do diagrama de Routh-Hurwitz.
Resposta
Duas raízes no semiplano direito