A função de transferência em malha fechada de um sistema é
Determine quantos polos em malha fechada estão no semiplano da direita, no semiplano da
esquerda e sobre o eixo .
Passo 1
Para aplicar o método de Routh-Hurwitz, precisamos definir a equação característica do sistema.
A equação característica do sistema é sempre o denominador da função de transferência em malha fechada. Portanto, a nossa equação característica será:
Devemos então elaborar o diagrama de Routh do sistema, seguindo o modelo:
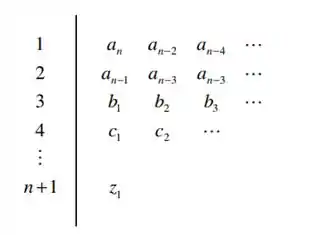
Passo 2
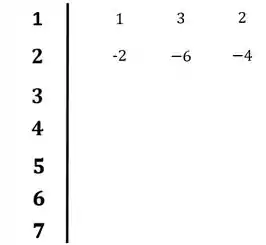
O primeiro passo, será preencher a primeira e a segunda linha com os coeficientes da equação característica:
Passo 3
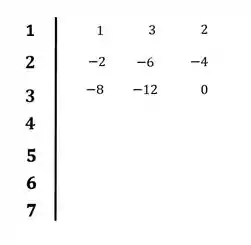
Vamos agora calcular os coeficientes da terceira linha conforme as expressões abaixo:
Colocando os valores no diagrama:
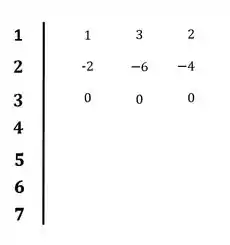
Vixi, demos de cara com uma linha de zeros. Para resolver isso, devemos utilizar o polinômio auxiliar, que é sempre retirado da linha anterior. Como a linha anterior é a segunda linha do diagrama e a equação característica do sistema tem ordem cinco, o polinômio auxiliar terá ordem quatro. Sendo assim ele será:
Lembra sempre que o polinômio auxiliar sempre pula um termo. Então se ele tem ordem quatro, ele não vai apresentar os termos de ordem ímpar.
Agpra precisamos derivar o nosso polinômio auxiliar:
Os coeficientes desse novo polinômio serão os números que colocaremos no lugar da linha de zeros.
Passo 4
Vamos então continuar calculando o nosso diagrama a partir daí.
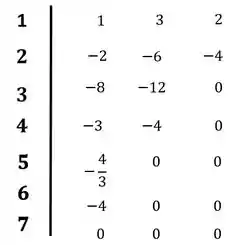
Vamos analisar o diagrama que obtivemos agora.
Existe uma troca de sinais entre a primeira e a segunda linha, o que indica a presença de um polo no semiplano direito.
Tivemos uma linha de zeros, e o nosso polinômio auxiliar foi:
Como o polinômio auxiliar foi de ordem 4, isso indica que temos 4 polos em simetria com relação à origem.
Entretanto, após a aparição da linha de zeros, não tivemos nenhuma troca de sinal, o que indica que nenhum dos polos em simetria está no semiplano direito, portanto, a única forma desses polos serem simétricos em relação à origem é estando os quatro sobre o eixo .
Portanto temos um polo no semiplano direito e quatro polos sobre o eixo .
Resposta
Um polo no semiplano direito e quatro polos sobre o eixo .