Considere um sistema com realimentação unitária e função de transferência mostrada abaixa.
Esboce o lugar as raízes e diga para quais valores de , o sistema é instável.
Passo 1
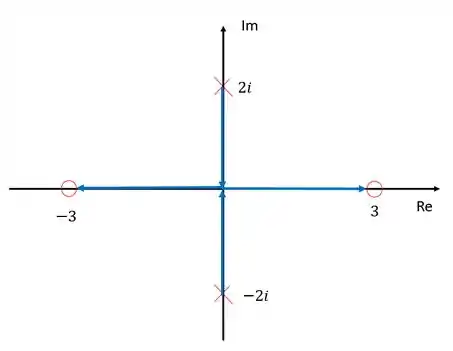
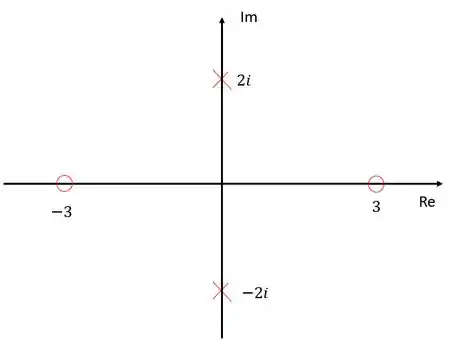
Primeiramente, vamos representar os polos e zeros no diagrama de lugar das raízes.
A função de transferência tem dois zeros: e , e dois polos: e .
Passo 2
Agora vamos fazer nosso nosso esboço.
Devemos nos lembrar que os ramos nascem nos polos e morrem nos zeros, e que a simetria com relação ao eixo dos reais deve ser obedecida.
Além disso, os ramos só podem existir sobre os eixos dos reais se a esquerda dele houver um número ímpar de polos e zeros.
Como os polos se enontram exatamente no meio do caminho entre os dois zeros, podemos garantir que os ramos vão entrar no eixo dos reais exatamente no meio do intervalo entre os dois zeros.
Tendo tudo isso em mente, já podemos esboçar nosso diagrama:
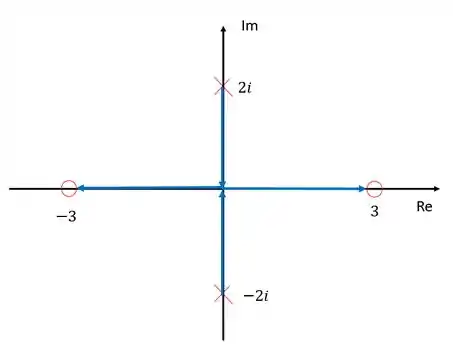
Passo 3
Agora, precisamos encontrar qual valor de faz com que o sistema fique instável. Vamos analisar a equação característica do sistema:
Para que o sistema seja estável, todos os termos devem ter o mesmo sinal. Não existe nenhum valor de que faça ambos os termos ficarem negativos, então vamos avaliar os valores de que faça os termos ficarem positivos:
Como no lugar das raízes trabalhamos com valores de que vão de até , podemos dizer que o sistema é instável para:
Resposta