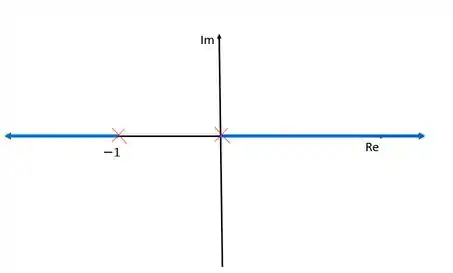
Esboce o lugar geométrico das raízes para um sistema com realimentação unitária positiva e a seguinte função de transferência em malha aberta:
Passo 1
Trata-se de um sistema com realimentação positiva, isso quer dizer que todas as regras que usamos até aqui são válidas com exceção de duas: o lugar das raízes existe no eixo dos reais se à sua esquerda existir uma quantidade par de polos e zeros, e a soma de todos os ângulos em qualquer ponto do lugar das raízes é um múltiplo par de .
Vamos começar, como sempre, representando os nossos polos e zeros no diagrama. Ness exercício temos dois polos: e .
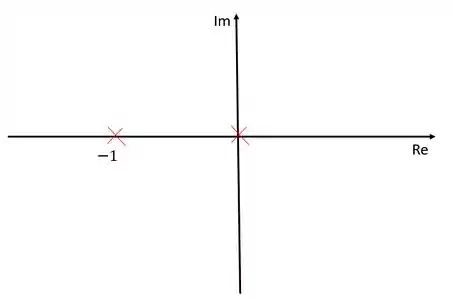
Passo 2
Nesse caso, temos dois polos a mais que zeros, o que significa que vamos ter dois zeros no infinito, e que precisaremos de duas assíntotas para nos mostrar onde esses zeros no infinito se encontram. Como é um sistema de realimentação positiva, a fórmula do ângulo da assíntota é um pouquinho diferente:
Repare que se , o ângulo é igual a , se , o ângulo será , e se r continuar aumentando, esses dois ângulos vão se repetir.
Sendo assim, teremos duas assíntotas sobre o eixo dos reais, cada uma apontando para uma direção.
Como as assíntotas estão sobre o eixo dos reais, não faz sentido calcular o ponto de interseção delas com essse eixo, concorda?
Passo 3
Agora, já temos tudo que precisamos e podemos fazer nosso esboço, olha só:
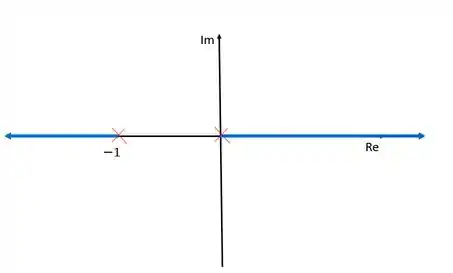
Como é um sistema de realimentação positiva, o lugar das raízes só existe se a sua esquerda houver um número par de polos e zeros. Por isso, não existe lugar das raízes entre os dois polos, uma vez que nesse intervalo só existe um polo à esquerda.
Como as assíntota indicam e , um dos ramos tede a sobre o eixo dos reais e o outro ramo tende a , também sobre o eixo dos reais.
Repare também que esse sistema é instável independente do valor de , já que não existe nenhum valor de que deixe as duas raízes negativas.
Resposta