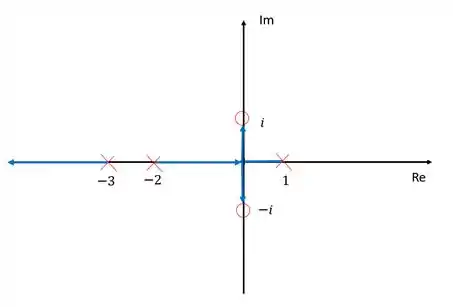
Esboce o lugar geométrico das raízes para um sistema com realimentação unitária e a seguinte função de transferência em malha aberta:
Passo 1
Primeiramente, vamos marcar no nosso diagrama todos os zeros e polos:
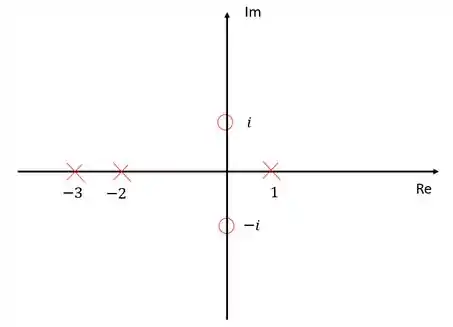
Passo 2
Temos um polo a mais que zero, o que significa que precisamos calcular uma assíntota que indique onde se encontra o zero no infinito.
Termos então uma assíntota com ângulo de que se encontrará sobre o eixo dos reais. Sendo assim, não precisamos calcular o ponto de interseção dessa assíntota sobre o eixo.
Passo 3
Vamos agora calcular o ponto em que o lugar das raízes deixa o eixo dos reais. Para isso precisamos maximizar na expressão:
Substituindo por , e derivando em relação a :
Existem dois valores para que satisfazem a igualdade: e , entretanto, não pode existir lugar das raízes em pois à esquerda desse ponto existem dois polos, e a condição para que exista lugar das raízes sobre o eixo real é que à esquerda deve existir sempre um número ímpar de zeros e polos.
Portanto, o lugar das raízes sairá do eixo dos reais em e para fins de esboço e práticos, vamos aproximar esse valor para .
Passo 4
Agora devemos encontrar o ângulo com que os ramos saem dos polos, para isso precisamos fazer a soma de todos os ângulos, o resultado deve ser um múltiplo ímpar de .
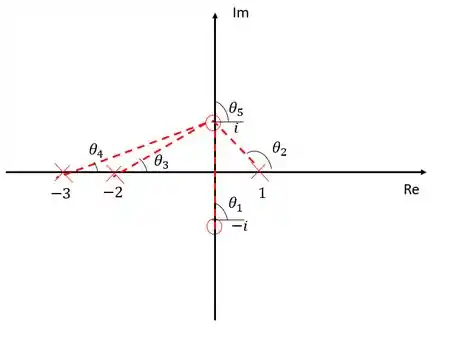
Para achar basta somar tudo e encontrar um ângulo cuja a soma seja um múltiplo ímpra de . Lembre-se sempre que os polos contribuem positivamente e os zeros negativamente:
Passo 5
Agora já podemos fazer nosso esboço:
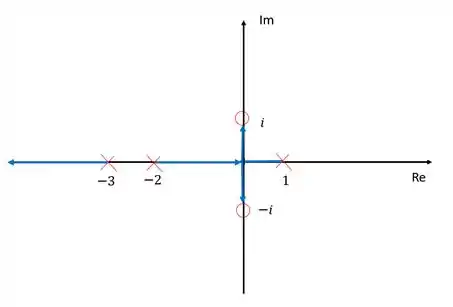
Os ramos que saem dos polos e saem do eixo dos reais em e morrem nos dois zeros finitos fazendo um ângulo de e .
Além disso, o ramo que nasce no em tende a infinito conforme a assíntota que calaculamos.
Resposta