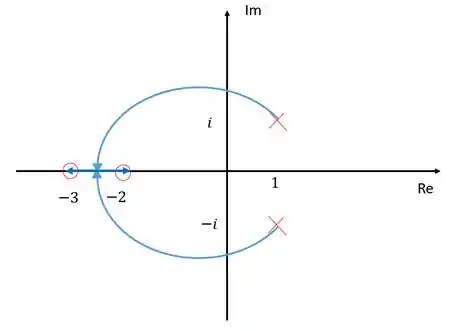
Para o diagrama de polos e zeros em malha aberta mostrado na figura abaixo, esboce o lugar geométrico das raízes e determine o ponto de entrada.
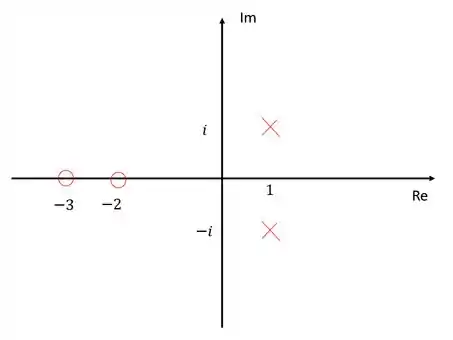
Passo 1
Temos então um diagrama de lugar das raízes de uma função de transferência em malha aberta com dois polos e dois zeros, sendo os zeros e , e os polos, .
Vamos então escrever a função de transferência para esse diagrama:
Passo 2
Nessa função temos dois polos e dois zeros, o que quer dizer que não teremos nenhum zero no infinito, então, não precisamos calcular as assíntotas.
Entretanto existem outras duas coisas que precisamos saber para fazer um bom esboço do diagarama de lugar das raízes: em que ponto o diagrama entre no eixo dos reais e com qual ângulo os ramos saem dos polos.
Se pensarmos um pouco sobre as regras que dizem que os ramos saem dos polos e morrem nos zeros, e que o diagrama é simétrico em relação ao eixo dos reais, poderemos imaginar que os ramos vão sair do polo e entrar no eixo dos reais em algum ponto entre os dois zeros, mas não sabemos com que ângulo essa saída se dá nem em que ponto eles entram no eixo dos reais.
Passo 3
Vamos começar pelo ponto de entrada.
Para isso, devemos maximizar\minimizar na expressão:
Isolando :
Substituindo por , e derivando em relação a , teremos:
Os valores de que satisfazem essa igualdade são e . Como o ponto de entrada está entre os dois zeros, o valor que nos satisfaz é .
Passo 4
Agora devemos encontrar o ângulo com que os ramos saem dos polos, para isso precisamos fazer a soma de todos os ângulos, o resultado deve ser um múltiplo ímpar de .
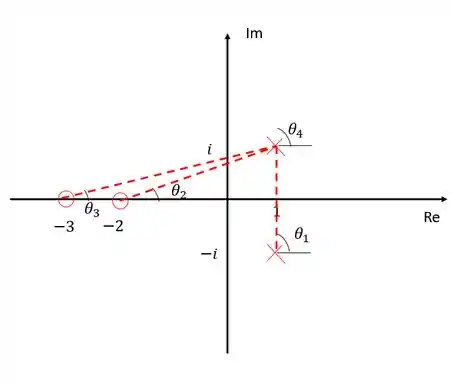
Para achar basta somar tudo e encontrar um ângulo cuja a soma seja um múltiplo ímpra de . Lembre-se sempre que os polos contribuem positivamente e os zeros negativamente:
Passo 5
Agora já podemos fazer nosso esboço:
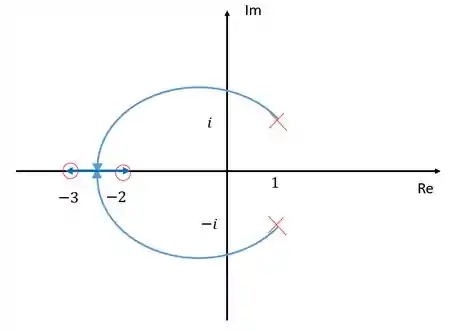
Resposta