Esboce o lugar geométrico das raízes e suas assíntotas para um sistema de retroalimentação unitária com a seguinte função de transferência:
Passo 1
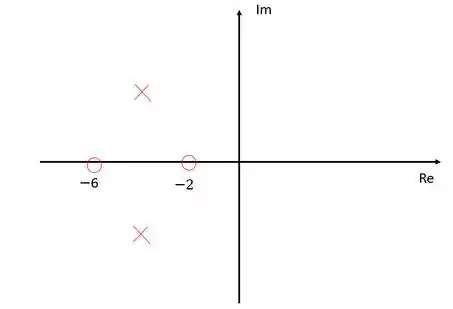
Vamos começar representando tanto os zeros como os polos da função de transferência em malha aberta no diagrama de lugar das raízes.
Para essa função de transferência temos dois zeros em e e dois polos em .
Passo 2
Neste caso o número de zeros finitos é igual ao número de polos infinitos, ou seja, não teremos zeros no infinito, e se não temos zeros no infinito, não precisamos calcular as assíntotas.
Além disso, como os polos estão exatamente no meio dos dois zeros, o lugar onde o rmo vai entrar no eixo dos reais é a metade do caminho entre e , ou seja, .
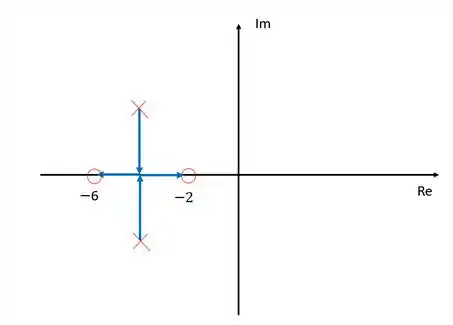
Desenhando os ramos:
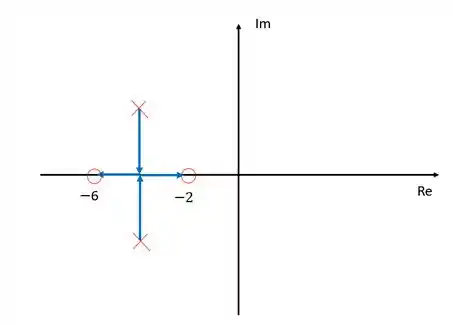
Nosso diagrama está obedecendo a todas as regras:
- Os ramos nascem nos polos e morrem nos zeros;
- O número de ramos é igual ao número de polos em malha aberta;
- Simetria em relação ao eixo dos reais existe;
- Só existe ramos sobre o eixo dos reais nos locais onde à esquerda existe um número ímpar de polos e zeros.
Portanto, nossa resposta está correta.
Resposta