Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 10.Perguntas e Problemas - Ex. 10

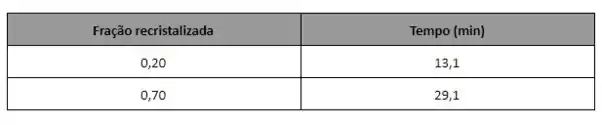
Abaixo estão relacionados os dados da fração recristalizada em função do tempo para a recristalização a 600℃ de um aço previamente deformado. Assumindo que a cinética desse processo obedece à relação de Avrami, determine a fração recristalizada após um tempo total de 22,8 min.

Passo 1

Fala aí galera, hoje vou ensinar vocês essa questão aqui que é muito massa!

A primeira coisa necessária é configurar duas expressões da forma da Equação 10.17 e, em seguida, resolver simultaneamente os valores de n e k. Para agilizar esse processo, reorganizarmos e faremos alguma manipulação algébrica da Equação 10.17. Primeiro, organizamos da seguinte maneira:

1 - y = e x p ( - k t n )

Agora tomando logaritmos naturais

l n ( 1 - y )   =   - k t n

Ou

- l n ( 1 - y ) = k t n

que também pode ser expresso como

l n ( 1 1 - y ) = k t n

Passo 2

Agora, tomando logaritmos naturais novamente, leva a

l n [ l n ( 1 1 - y ) ] = l n k + n l n t

que é a forma da equação que usaremos agora. As duas equações são assim:

l n { l n [ 1 1 - 0.20 ] } = l n k + n l n   ( 13.1   m i n )

l n { l n [ 1 1 - 0.70 ] } = l n k + n l n ( 29.1   m i n )

Passo 3

Resolver essas duas expressões simultaneamente para n e k produz n = 2,112 e k = 9.75 × 1 0 - 4 . Agora torna-se necessário resolver y quando t = 22,8 min. A aplicação da Equação 10.17 leva a

y = 1 - e x p ( - k t n ) = 1 - e x p [ - ( 9.75 × 1 0 - 4 ) ( 22.8   m i n ) 2.112 ] = 0.51

Resposta

y = 0.51

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma dada transformação com uma cinética que obedece à equação de Avrami (Equação 10.17), sabe-se que o parâmetro n tem valor de 1,7. Se após 100s a reação está 50% completa, quanto tempo (tempo t
Considere para a solidificação do ferro (Problema 10.4) que a nucleação seja homogênea e que o número de núcleos estáveis seja de 1 0 6 núcleos por metro cúbico. Calcule o raio crítico e o número de n
Sabe-se que a cinética da recristalização para uma dada liga obedece à equação de Avrami e que o valor de n na exponencial é de 2,5. Se a uma dada temperatura a fração recristalizada equivale a 0,40 d
Calcule a taxa de uma dada reação que obedece à cinética de Avrami, assumindo que as constantes n e k têm valores de 3,0 e de 7 × 1 0 - 3 , respectivamente, sendo o tempo expresso em segundos.
Para a solidificação do ferro, calcule o raio crítico r * e a energia livre de ativação Δ G * se a nucleação é homogênea. Os valores para o calor latente de fusão e para a energia livre de superfície