Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 49
Um corpo de provas cilíndrico feito de latão, com de diâmetro e de comprimento, é tracionado com uma força de ; a seguir, a força é liberada.
- Calcule o comprimento final do corpo de provas nesse instante. O comportamento tensão deformação em tração para essa liga está mostrado na Figura .
- Calcule o comprimento final do corpo de provas quando a carga é aumentada para e então liberada.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Pessoal, nesse exercício, temos que calcular o comprimento final de um corpo de provas em duas situações.
No item (a) o corpo é tracionado com uma força de e no item (b) o corpo é tracionado com uma força de .
Nos foi dito que o comportamento de tensão deformação para esta liga corresponde ao gráfico abaixo:
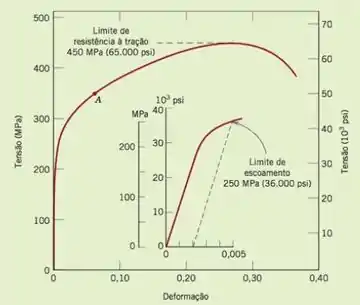
Ou seja... Temos que calcular a tensão em cada caso e descobrir qual a deformação gerada... Bem simples né? Vamos lá.
Passo 2
A equação para o cálculo da tensão é dada por:
Onde é a carga e é a área da seção transversal.
Como a amostra é cilíndrica, temos que:
Onde é o diâmetro inicial da seção transversal.
Portanto, a equação da tensão pode ser dada por:
No exercício nos foi dito que o diâmetro inicial do corpo de prova é de .
Passo 3
Portanto, para o item (a), temos que:
Vamos avaliar no gráfico qual a deformação correspondente para esta tensão.
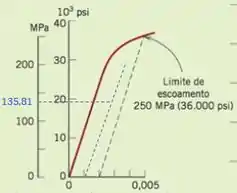
Podemos observar que o corpo sofreu somente deformação elástica, portanto o corpo não deformou plasticamente e continuou com o seu comprimento original após a carga ser liberada.
Passo 4
Para o item (b), temos que:
Vamos avaliar no gráfico qual a deformação correspondente para esta tensão.
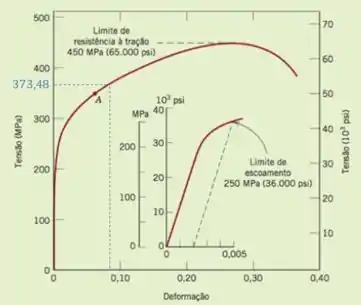
Podemos observar que o corpo sofreu deformação plástica. Desenhando uma linha reta paralela à região elástica linear, podemos observar que a deformação correspondente é de cerca de .
O comprimento final pode ser calculado a partir da seguinte equação:
Substituindo os valores, temos que:
Portanto, o comprimento final da amostra é de .