Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 48
Tirando o logaritmo de ambos os lados da Equação , tem-se
Dessa forma, um gráfico de em função do na região plástica, até a estricção, deve produzir uma linha reta com inclinação e ponto de interseção (em ) .
Usando os dados apropriados tabulados no Problema , trace um gráfico de em função de e determine os valores de e . Será necessário converter as tensões e deformações de engenharia em tensões e deformações verdadeiras utilizando as Equações e .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Pessoal, nesse exercício, temos que plotar um gráfico de em função do na região plástica até a estricção.
Este gráfico deve ser uma reta que tem inclinação e ponto de interseção (em ) .
O gráfico deve ser plotado a partir dos dados tabulados do Problema :
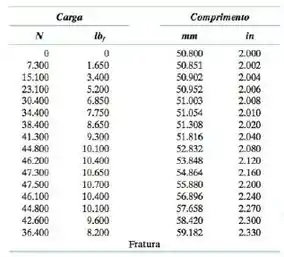
Podemos usar o Software “EXCEL” para isto.
Passo 2
No EXCEL insira os dados correspondentes à zona plástica que se inicia na carga de e comprimento de .
A tensão verdadeira é dada por:
E a deformação verdadeira é dada por:
Portanto, precisamos encontrar a tensão e a deformação de Hooke primeiro. Temos que:
Onde é a carga e é a área da seção transversal.
Como a amostra é cilíndrica, temos que:
Onde é o diâmetro da seção transversal.
Portanto, a equação da tensão pode ser dada por:
A equação para a deformação é dada por:
Onde é o comprimento correspondente a cada carga aplicada e o comprimento inicial.
Passo 3
Inserindo os dados no EXCEL e as determinadas funções, podemos construir a seguinte tabela:
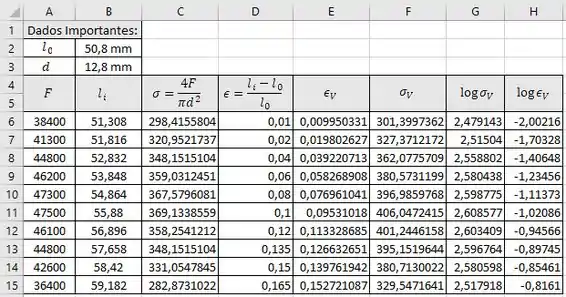
O ponto de estricção se inicia com a carga de , portanto, para o gráfico utilizaremos apenas os primeiros valores. Essa será nossa zona plástica até a estricção. Teremos o seguinte gráfico:
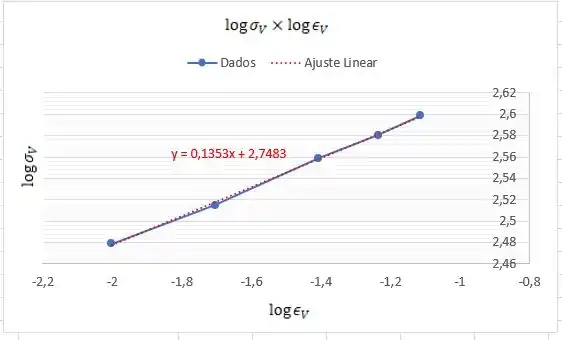
Passo 4
Como podemos observar a inclinação da reta é dada por:
De acordo com a equação do ajuste linear, quando , temos que:
Ou:
Portanto, podemos descobrir o valor de a partir da equação:
Portanto o valor de será: