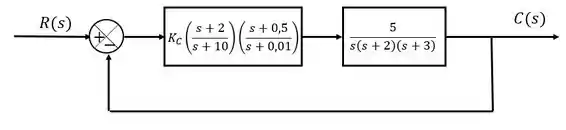
Dado o sistema de controle acima, calcule o ganho do compensador sabendo que é desejado que o polo dominante seja:
Passo 1
Primeiramente, vamos representar todos os polos e zero no diagrama de lugar das raízes.
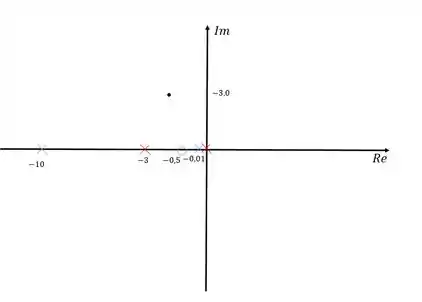
Como o compensador tem um zero em e também existe um polo nesse mesmo ponto, podemos fazer um cancelamente polo/zero.
Passo 2
Vamos agora, calcular as distâncias desses polos e zeros até o polo dominante:
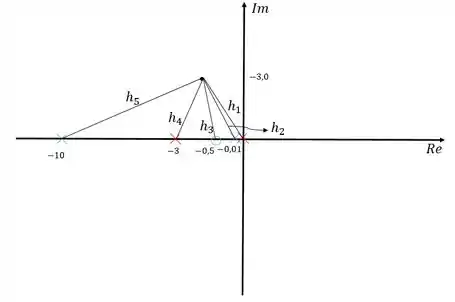
Usando o Teorema de Pitágoras:
O ganho poderá ser calculado da seguinte maneira:
O ficou no numerador pois é o único zero que estamos avaliando.
é o ganho da função de transferência em malha aberta, nesse caso, e é o ganho do compensador que desejamos encontrar: