Dado o sistema com realimentação unitária, sem compensação mostrado abaixo
Projete um compensador para resultar nas seguintes especificações: tempo de acomodação de ; ultrapassagente percentual de e o erro em regime permanente deve ser igual a para uma entrada em rampa.
Passo 1
Vamos começar com as especificações da resposta transitória que vão nos dar as informações que precisamos para determinar o polo e zero da parte de avanço do compensador.
Para isso, precisamos primeiramente determinar os polos dominantes em malha fechada do sistema compensado, ou seja, os polos dominantes que produzirão o overshoot e o tempo de acomodação desejados.
O polo dominante poderá ser encontrado através da expressão:
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Como queremos um overshoot de :
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Como
Portanto, o polo dominante será:
Passo 2
Vamos representar no nosso diagrama agora como estamos até aqui. Vamos colocar os polos dominantes da resposta compensada e também os polos da função de transferência do processo.
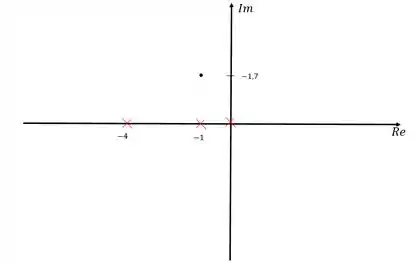
Os “x” vermelhos são os polos em malha aberta da função de transferência, e o ponto preto é um dos polos dominantes que vamos usar no nosso projeto.
Vamos então começar a implementar o nosso avanço. Para isso precisamos arbitrar um valor para o zero e depois encontrar o valor para o polo.
Para diminuir o número de contas, podemos colocar o zero do compensador “em cima” de um dos polos em malha fechada para que o zero cancele esse polo. Sendo assim:
Sendo o zero da parte do avanço do compensador. Para determinar o polo da parte de avanço, precisamos usar a regra dos ângulos aqui:
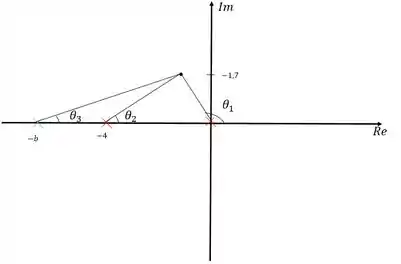
Não temos mais o polo em pq ele foi cortado com o zero do compensador. O polo do compensador que precisamos determinar, está representado pelo . Para saber onde ele está, usaremos a regra dos ângulos
Ou seja, a soma de todos os ângulos deve ser um múltiplo ímpar de .
Para calcular os ângulos, usaremos propriedades trigonométricas:
Sendo assim:
E com o ângulo , conseguimos determinar a posição de :
Portanto o polo da parte de avanço do compensador está em .
Sendo assim já determinamos o polo e o zero da parte de avanço, e ainda falta determinar o ganho, o polo e o zero do compensador.
Passo 3
Antes de partir para a parte do atraso, vamos calcular o ganho do compensador. Para isso, usaremos o critério do módulo:
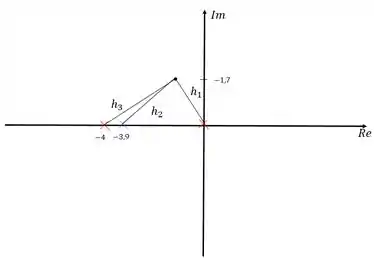
Usando o Teorema de Pitágoras, podemos calcular as distâncias , e :
Sendo assim, o ganho será:
Onde é o ganho da função de transferânecia em malha aberta que neste caso é .
Portanto, estamos assim com o nosso projeto:
Só falta então encontrar o polo e zero do atraso.
Passo 4
Para implementar o compensador de atraso, precisamos encontrar a relação entre o zero e o polo que falta determinar.
Para uma entrada rampa, teremos a seguinte expressão para o erro:
Como queremos que o erro em estado permanente seja devemso fazer com que a igualdade abaixo seja verdade:
Substituindo o que temos:
Teremos que:
Ou seja, o zero dever ser maior que o polo por um fator de vezes para que o erro em regime estacionário do sistema compensado seja 20 vezes menor que o do sistema não compensado.
Sabemos que o polo e o zero do compensador de atraso devem ser o menor possível para não impactar na resposta transiente. Portanto, um bom valor para esse par seria:
Portanto, teremos:
Passo 5
Dessa vez, como o zero do compensador foi muito maior que o polo, vamos recalcular o nosso ganho para garantir que não houve um desvio muito grande. Sendo assim, vamos aplicar novamente o critério do módulo mas dessa vez considerando o polo e o zero novos.
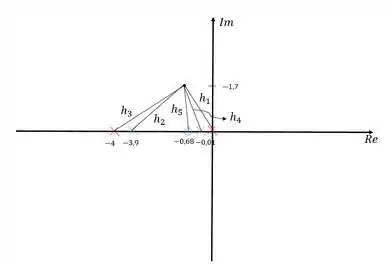
Como já temos , e , vamos calcular e :
Sendo assim, o ganho será:
Dessa vez a diferença no ganho não foi tão significante, mas o seguro morreu de velho não é mesmo?
Finalmente, o nosso compensador será: