Dado o sistema com realimentação unitária, sem compensação mostrado abaixo
Projete um compensador para resultar nas seguintes especificações:
Overshoot: ;
Tempo de acomodação para uma faixa de : ;
Erro em regime permanente para uma entrada degrau: .
Passo 1
Vamos começar projetando a parte de avanço do nosso compensador. Vamos fazer isso da mesma forma que fazíamos quando estavámos projentando um compensador de avanço de fase simples. Bora lá!
Primeiramente, precisaremos determinar os polos dominantes em malha fechada do sistema compensado, ou seja, os polos dominantes que produzirão o overshoot e o tempo de acomodação desejados.
O polo dominante poderá ser encontrado através da expressão:
Para encontrar e usaremos as especificações do projeto.
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Como queremos um overshoot de :
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Como
Portanto, o polo dominante será:
Passo 2
Vamos então representar no diagrama de lugar das raízes os dois polos dominantes e também os polos e zeros da nossa função de transferência em malha aberta. Nesse caso, a função só tem polos e ficaremos com a seguinte representação:
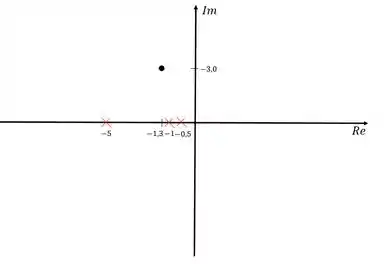
Vamos usar os “x” vermelho para representar os polos do compensador e o ponto preto é o polo dominante que nós encontramos, mas eu representei no diagrama só um dos dois polos porque para fazer o projeto é necessário apenas um.
Quando estamos projetando m compensador de avanço podemos arbitrar a posição do zero e fazer com que o polo obedeça essa posição encontada.
E já que podemos escolher qualquer posição para o zero, a gente que não é bobo nem nada vai escolher uma posição que beneficia a gente. Se colocarmos o zero do compensador na mesma posição que um do polos. O zero vai cancelar o polo e então teremos menos pontos para trabalhar no projeto. Sendo assim, vamos assumir:
Agora que arbitramos a posição do zero, vamos encontrar o zero através da regra dos ângulos:
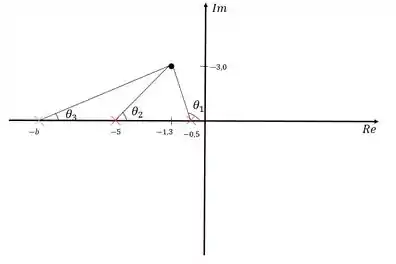
Não temos mais o polo em pq ele foi cortado com o zero do compensador. O polo do compensador que precisamos determinar, está representado pelo . Para saber onde ele está, usaremos a regra dos ângulos
Ou seja, a soma de todos os ângulos deve ser um múltiplo ímpar de .
Para calcular os ângulos, usaremos propriedades trigonométricas:
Sendo assim:
E com o ângulo , conseguimos determinar a posição de :
Portanto o polo da parte de avanço do compensador está em .
Sendo assim já determinamos o polo e o zero da parte de avanço, e ainda falta determinar o ganho, o polo e o zero do compensador.
Passo 3
Antes de partir para a parte do atraso, vamos calcular o ganho do compensador. Para isso, usaremos o critério do módulo:
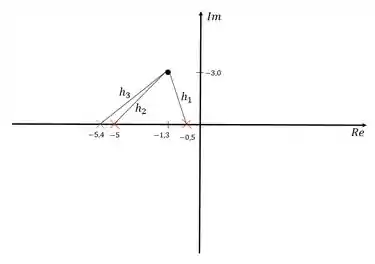
Vamos calcular as distâncias , e :
Sendo assim, o ganho será:
Sendo o ganho da função de transferência em malha aberta, nesse caso, e o ganho do compensador que desejamos encontrar:
Portanto, estamos assim com o nosso projeto:
Só falta então encontrar o polo e zero do atraso.
Passo 4
Para implementar o compensador de atraso, precisamos encontrar a relação entre o zero e o polo que falta determinar. Para isso usaremos a especificação do erro em regime permanente.
Para uma entrada degrau unitário, teremos a seguinte expressão para o erro:
Como queremos que o erro seja igual a teremos:
Com isso, conseguimos obter:
Ou seja, o zero dever ser maior que o polo por um fator de 3,4vezes para que o erro em regime estacionário do sistema compensado seja igual a .
Sabemos que o polo e o zero do compensador de atraso devem ser o menor possível para não impactar na resposta transiente. Portanto, um bom valor para esse par seria:
Portanto, teremos:
Se quiséssemos ser muito precisos, poderíamos calcular novamente o ganho usando o critério do módulo. Entretanto a inclusão do novo polo e do novo zero quase não alterariam o ganho encontrado anteriormente uma vez que eles têm o módulo praticamente iguais por estarem muito próximos um do outro, e portanto, se anulariam. Sendo assim, para nós o projeto já está satisfatório.