Considerando a função de transferência do processo abaixo:
Projete um compensador de avanço de fase de modo que o overshoot máximo seja e o tempo de sedimentação para um critério de seja .
Passo 1
O pimeiro passo para projetar o compensador é definir umpar depolos dominantes de malha fechada que atenda às necessidade requeridas. Para definir o polo dominante, precisamo de e :
Podemos calcular através da fórmula do overshoot:
Para um overshoot de máximo de , teremos:
Fazer o projeto com o fator de amortecimento no limite é um pouco arriscado, visto que essas equações são aproximações e o resultado final pode variar um pouco. Sendo assim, vamos dar uma folguinha para o fator de amortecimento e usar:
Para achar utilizaremos a expressão para tempo de sedimentação com critério de :
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
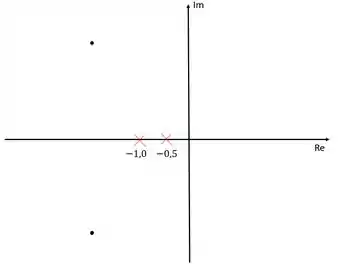
Os polos da função de transferência estão representados com um “xis” vermelho. Os polos dominantes estão representados pelos pontos.
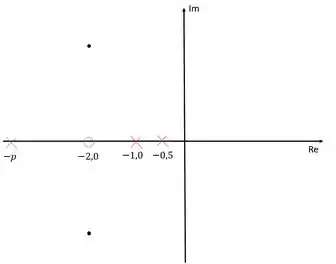
Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do lugar das raízes. Existem infinitas combinações para esse polo e zero. Sendo assim, vamos arbitrar um valor para o zero e calcular o polo depois a partir desse valor de arbitrado do zero.
Uma tática é colocar o zero sobre o eixo dos reais com o mesmo valor do polo dominante. Então vamos fazer isso, vamos assumir que o zero se encontra em . Vamos fazer usando essa tática então:
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
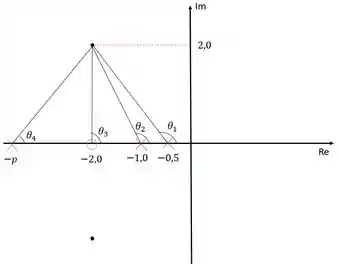
Para conseguir o ângulo , precisamos calcular os ângulos , e . Podemos calcular esses ângulos utilizando o arcotangente deles. Então vamos lá:
Como está diretamente abaixo do polo dominante:
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
Lembrando que os polos contribuem com ângulos negativos e os zeros com ângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
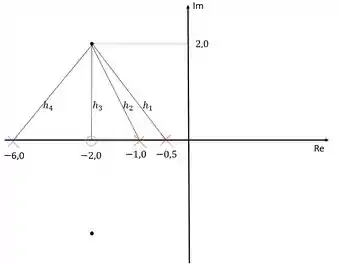
Obs: a figura não está representada em escala.
Dessa forma:
Portanto:
Os zeros ficam no numerador e os polos no denominador: