Considere um sistema com realimentação unitária função de transferência do processo:
- Determine a posição dos polos dominantes para resultar em um tempo de acomodação de e emum overshoot de .
- Se um compensador com o zero em for utilizado para alcançar as condições do item a), qual deve ser a contribuição angular do polo do compensador?
- Determine a posição do polo do compensador.
- Determine o ganho necessário para atender aos requisitos declarados no item a).
Passo 1
Para determinar a posição dos polos dominantes para as especificações dadas, precisamos calcular e que tornam esses requisitos verdadeiros. Uma vez que obtemos esses valores, os polos dominantes podem ser calculados pela fórmula:
Podemos calcular através da fórmula do overshoot:
Para um overshoot de , teremos:
Para achar utilizaremos a expressão para tempo de sedimentação com critério de :
Os polos dominantes são portanto:
Passo 2
O item b) pede que seja calculado a contribuição de ângulo do polo de um compensador projetadopara atingir essas condições e com zero em . Vamo representar tudo isso no diagrama de lugar das raízes então:
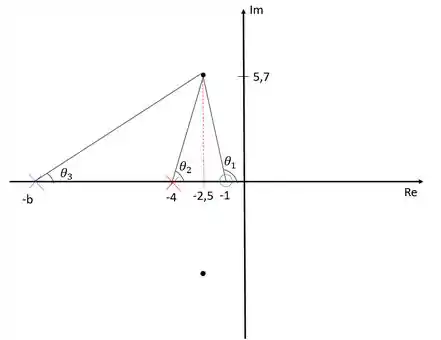
Para definir o ângulo , precisamo primeiro descobrir e . Sendo assim:
No lugar das raízes, a soma de todos os ângulo feitos entre os zeros e polos e qualquer ponto por onde passa o lugar das raízes deve ser um múltiplo ímpar de . Como desejamos que o lugar das raízes passe pelo nosso polo dominante, a soma de todas os ângulos deve satistafzer essa igualdade.
Obs: O ângulo é multiplicado por três porque o polo em é de terceira ordem.
Passo 3
Para determinar a posição do polo, utilizaremos a tangente do módulo ângulo :
Como é a distância entre o polo e o ponto , o polo estará em .
Passo 4
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
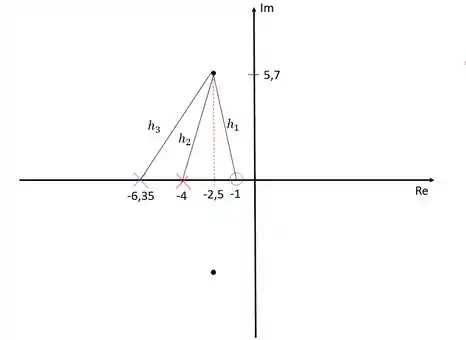
Dessa forma:
Sendo assim:
está elevado ao cubo, devido ao fato de o polo em ser de terceira ordem.
Portanto: