Para um sistema realimentado, a função de transferência em malha aberta é:
Projetar um controlador tal que o tempo de sedimentação seja e o overshoot máximo seja de .
Passo 1
Precisamos determinar , e da função de transferência do compensador que satisfaça os critérios do enunciado.
O primeiro passo é definir o polo dominante, e para isso precisamos de e .
Podemos calcular através da fórmula do overshoot:
Para um overshoot de , teremos:
Como o overshoot precisa ser menor que vamos dar uma folguinha e usar um valor um pouco acima do valor encontrado para , dessa forma, garantimos que o overshoot não ultrapassará o limite preestabelecido :
Para achar utilizaremos a expressão para tempo de sedimentação com critério de :
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
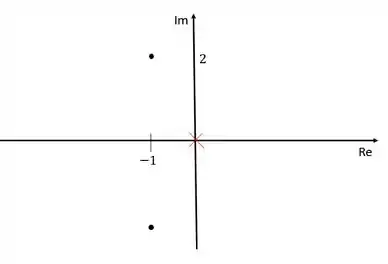
Os dois polos da função de transferência estão representados com um “xis” vermelho. Como os dois polos se encontram na origem, tem apenas um “xis” no gráfico, mas mantenha em mente que são dois polos. Os polos dominantes estão representados pelos pontos.
Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do local das raízes. Existem infinitas combinações para esse polo e zero. Sendo assim, vamos arbitrar um valor para o zero e calcular o polo depois a partir desse valor de arbitrado do zero.
Uma tática é colocar o zero sobre o eixo dos reais com o mesmo valor do polo dominante. Então vamos fazer isso, vamos assumir que o zero se encontra em .
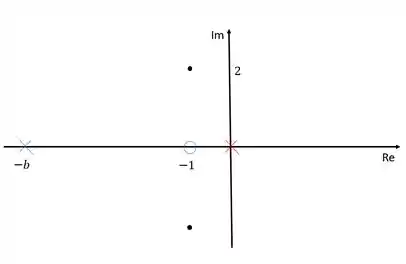
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
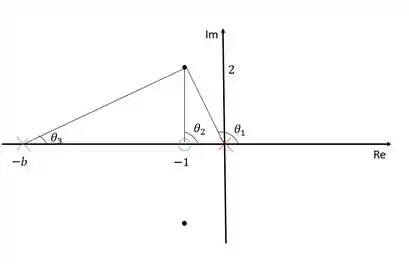
Para conseguir o ângulo , precisamos calcular os ângulos e . Podemos calcular esses dois ângulos utilizando o arcotangente deles. Então vamos lá:
O ângulo é visto que está na mesma linha horizontal que o polo dominante.
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
O ângulo tem que ser considerado duas vezes porque existem dois polos na origem.
Lembrando que os polos contribuem com ângulos negativos e os zeros com ângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
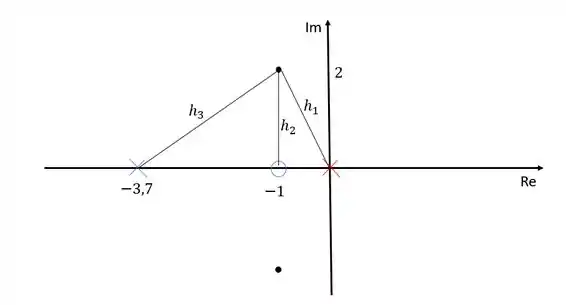
Dessa forma:
Portanto:
O termo referente a distância está ao quadrado devido à presença de dois polos na origem.