Dado o sistema realimentado com , projete um compensador digital que atenda às especificações:
Passo 1
O primeiro passo para fazer o projeto no plano é encontrar os polos dominantes no plano e depois convertê-lo ao plano .
O polo dominante no plano terá forma:
O valor de nós já temos que foi dado como especificação de projeto, . Para achar vamos usar a especificação do tempo de assentamento. Para uma faixa de a fórmula para o tempo de decaimento é a seguinte:
Substituindo os valores:
Os polos dominantes no plano serão portanto:
Passo 2
Agora precisamos determinar onde estarão esses polos no plano atravé das seguintes fórmulas:
Portanto, podemos calcular o módulo e o ângulo do polo no plano :
Portanto, o polo no plano em coordenadas angulares será:
Fazendo a conversão de coordenadas polares para retangulares teremos:
Passo 3
Vamos representar os polos dominantes e o polo da função de transferência do processo no diagrama abaixo:
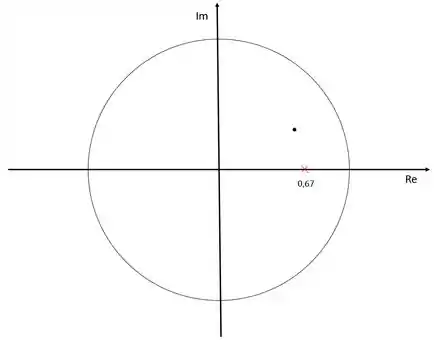
O ponto preto indica o polo dominante em e o “xis” vermelho representa o polo da função de transferência do processo. Agora precisamos encontrar o polo e o zero do compensador. Para isso, podemos simplesmente arbitrar um polo qualquer e então encontrar onde vai estar o zero correspondente.
Como o nosso compensador será de avanço sabemos que o polo tem que estar mais à direita que o zero. Sendo assim, vamos tentar arbitrar o nosso polo um pouco mais à direita do nosso diagrama.
Eu vou escolher simplesmente porque eu quero, mas você poderia ter escolhido qualquer valor para o polo. Sendo assim, vamos representar nosso diagrama agora:
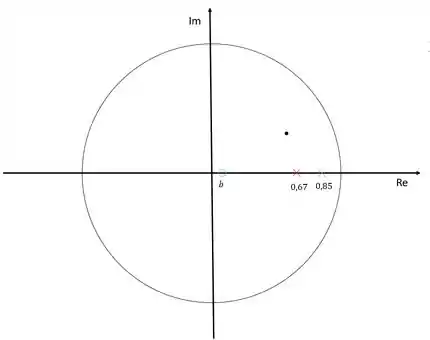
O “xis” azul representa o polo do compensador e o círculo azul o zero. O zero do compensador foi colocado em um lugar arbitrário, sendo assim, precisamos determiner qual é o ponto exato do zero considerando que o polo foi colocado em .
Passo 4
Para determinar o ponto exato do zero, usaremos a regra dos ângulos que diz que a soma dos ângulos dos polos menos a soma dos ângulos dos zeros deve ser igual a um múltiplo ímpar de .
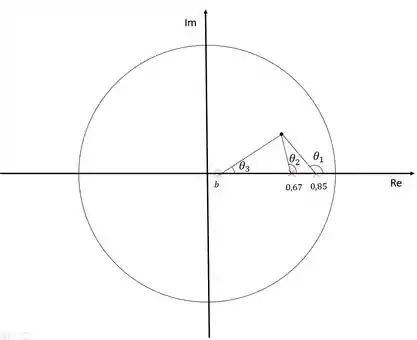
Sendo assim, teremos:
Vamos calcular os ângulos e :
Sendo assim, podemos determinar :
Podemos agora determinar o ponto exato do zero do compensar, já que encontramos o ângulo que ele faz com o polo dominante:
Isso vais nos dar:
Portanto, nosso compensador por enquanto está assim:
Falta apenas calcular o ganho.
Passo 5
Para calcular o ganho, usaremos o critério do módulo. Para isso, precisaremos calcular as distâncias entre os polos dominantes e os polos e zeros do sistema:
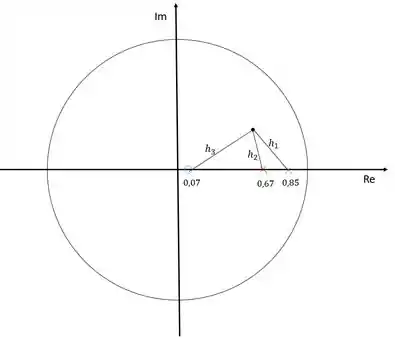
Precisamos calcular , e :
A regra do módulo diz que:
Sendo o ganho do compensador e o ganho do processo. Sendo assim:
Sendo assim, calculamos finalmente a função de transferência do nosso compensador de avanço: