A entrada de um controlador PI sofre uma modificação degrau do tipo C(s) = 2/s , onde C(s) é a variável controlada, e a saída do controlador (em relação ao estado estacionário) muda inicialmente conforme ilustrado na Figura seguinte. De acordo com a figura, estime os valores do ganho do controlador 𝐾𝐶 e a constante de tempo integral τ𝑖 . Considere que o set-point é fixo.
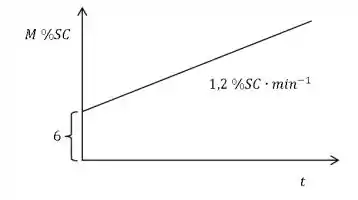
Passo 1
Para resolver essa questão bem rapidinho, vamos comparar o gráfico do enunciado, com esse gráfico aqui:
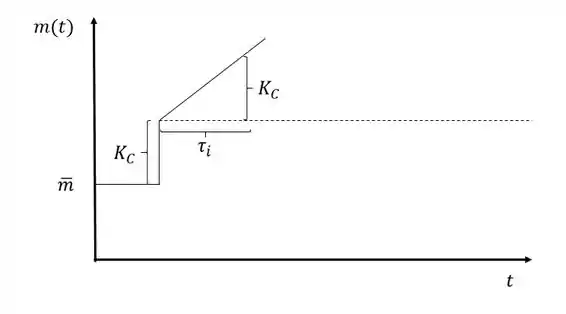
Esse gráfico é o gráfico da saída do controlado PI para uma resposta do tipo degrau unitário.
Passo 2
Pelo gráfico podemos perceber que é a variação no sinal no momento da perturbação. Entretanto, para o gráfico acima, a entrada foi um degrau unitário, já para o nosso exemplo, a entrada teve magnitude , sendo assim:
Mas, podemos perceber também que o controlador é do tipo direto, já que o um degrau positivo causou um aumento do sinal, sendo assim:
Passo 3
Pelo gráfico, também podemos perceber que a inclinação da reta é dada pela razão entre o ganho e a constante de tempo de integração. Então:
Novamente dividimos por devido à amplitude do degrau.