Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Defeitos Substitucional

Ver Teoria
Exercício 4123567891011

Enunciado

Calcule o raio do maior átomo que pode se situar no interstício octaédrico do Fe CFC, sem deformar a estrutura. Considere o raio do Fe como sendo 0.129nm.

Passo 1

Vamos desenhar uma face da estrutura CFC.

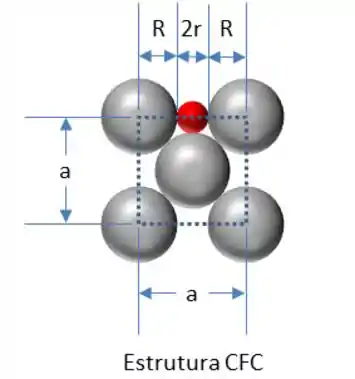
Conforme figura acima vemos que:

a 2 + a 2 = 4 ∙ R 2

2 ∙ a 2 = 16 ∙ R 2

a = 2 ∙ R ∙ 2 –> Equação 1

Nota-se também que:

a = 2 ∙ R + 2 ∙ r

r = a 2 - R

Passo 2

Agora vamos substituir a da equação acima pelo da equação 1 teremos:

r = 2 ∙ R ∙ 2 2 - R

r = R ∙ 2 - R

r = R ∙ 2 - 1 ≅ R ∙ 0414

Passo 3

Neste passo somente substituímos o valor do raio atômico do Fe para determinarmos o raio do maior átomo que poderá preencher o interstício da estrutura CFC do Fe:

r ≅ 0.129 ∙ 0414 = 0.053 n m

Resposta

r = 0.053 n m