Para as estruturas cristalinas CFC E CCC existem dois tipos de sítios intersticiais diferentes. Em cada caso, um sítio é maior que o outro e está normalmente ocupado por átomos de impurezas. Na estrutura CFC, esse sítio maior está localizado no centro de cada umas das arestas da célula unitária; ele é denominado sitio intersticial octaédrico. Por outro lado, na estrutura CCC, o maior tipo de sítio é encontrado nas posições 0 ½ ¼ - isto é, sobre as faces {1 0 0} – e situado sobre essa face a meio caminho entre duas arestas da célula unitária e a um quarto da distância entre as outras duas arestas da célula unitária; ele é denominado sítio intersticial tetraédrico. Tanto para a estrutura cristalina CFC quanto para a estrutura CCC, calcule o raio r de um átomo de impureza que irá se ajustar exatamente nesses sítios, em função do raio atômico R do átomo hospedeiro.
Passo 1
Vamos desenhar uma face da estrutura CFC.
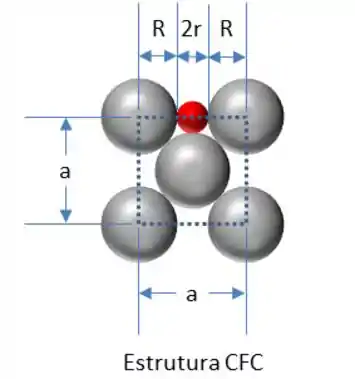
Conforme figura acima vemos que:
–> Equação 1
Nota-se também que:
Substituindo da equação acima pelo da equação 1 teremos:
Passo 2
Agora vamos desenhar uma face da estrutura CCC.
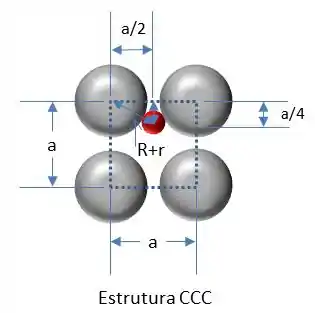
Sabemos, de capítulos anteriores, que o comprimento da célula unitária para a estrutura CCC é:
-> Equação 2
Pela figura acima temos:
Substituindo o valor de da equação 2 na equação acima teremos:
Resolvendo a equação para r:
Como deve ser maior do que zero, então:
Resposta
Ei, a resposta está no passo a passo :)