Dada a seguinte função de transferência:
- Faça um esboço das assíntotas da parte de razão de amplitude do diagrama de Bode.
- Indique o atraso de fase (ou avanço) em altas frequências .
Passo 1
O item a) pede que a gente construa somente a parte de razão de amplitude do diagrama de Bode. Então vamos lá.
A função de transferência já veio do jeito que a gente gosta, naquele formato tanto no polo quanto no zero, então não precisamos multiplicar/dividir a função de transferência por nada.
Sendo assim, já podemos substituir por :
A expressão para a razão de amplitude será:
Passo 2
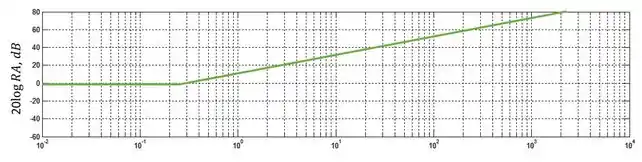
O primeiro termo é o termo referente ao zero. Sendo assim, em frequências baixas a razão de amplitude será e a partir da frequência de quebra, a razão de amplitude começará a subir a uma taxa de . A frequência de quebra nesse caso será . Vamos representar esse termo com uma linha verde no diagrama:
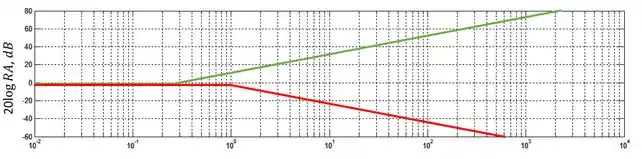
O segundo termo, que é referente ao polo, assim como o primeiro será em frequências baixas. Entretanto, ao contrário do zero, a partir de sua frequência de quebra, o polo começa a decair a uma taxa de . Para esse caso, a frequência de quebra será . Vamos representar esse segundo termo usando uma linha vermelha:
Passo 3
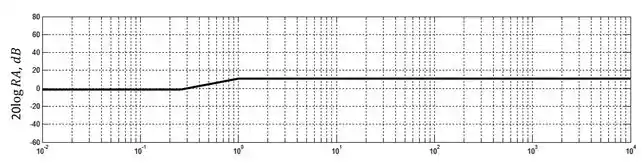
Agora que já representamos tanto o polo quanto o zero. Só precisamos juntar as duas linhas:
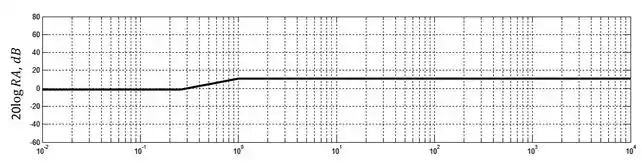
Entre e a razão de amplitude é pois a frequência é muito baixa tanto para o polo quanto para o zero exercerem qualquer tipo de influência. A partir de os efeitos do zero começam a ser sentidos e a razão de amplitude começa a se elevar, entretanto, em , o efeito do polo também começa a se fazer presente, se anulando com o efeito do zero e mantendo a razão de amplitude constante.
Passo 4
O item b) pergunta qual o avanço\atraso de fase da função de transferência em altas frequências.
Apesar de não termos esboçado a parte do diagrama de Bode para o ângulo de fase, é possível prever essa resposta se pensarmos um pouco sobre a estrutura da função de transferência.
A função de transferência em questão apresenta um polo, de primeira ordem, e um zero, também de primeira ordem. Vamos pensar como o polo e o zero se comportam em altas frequências.
O zero em baixas frequências tem ângulo de fase e em altas frequências, . Já o polo é o oposto, em baixas frequências ele também tem ângulo de fase , mas em altas frequências o ângulo de fase se torna .
Sendo assim, em altas frequências teremos o efeito de um polo, , e de um zero, . Quando combinamos os dois o ângulo de fase resultante é . Portanto:
Resposta