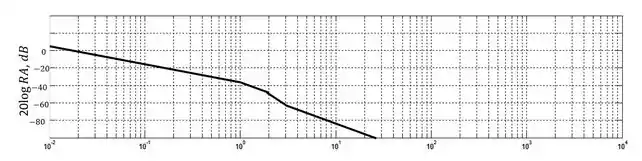
Esboce o diagrama de Bode da razão de amplitude da função de transferência abaixo:
Passo 1
Bora lá então. O primeiro passo é deixar todos os polos e zeros no formato , como o polo que tá na origem não tem como ficar nesse formato, então não fazemos nada com ele.
Para calcular a razão de amplitude e o ângulo de fase, precisamos substituir por :
A expressão para razão de amplitude, em , vai ficar:
Portanto:
Passo 2
Começando pela razão de amplitude.
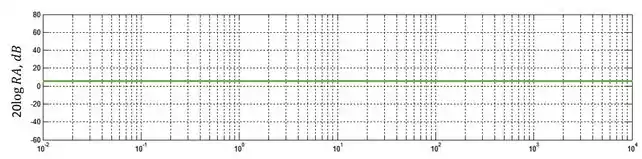
Para representar a razão de amplitude da função de transferência, devemos representar cada um dos termos separadamente e depois somar tudo. O primeiro termo é uma constante e será representado por uma linha verde:
Passo 3
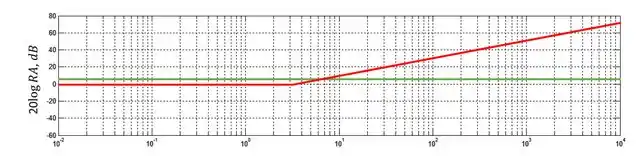
O segundo termo é o termo referente ao zero da função de transferência. Ele será em frequências baixas e uma reta com inclinação a partir da frequência de quebra que é . A inclinação é positiva porque se trata de um zero. Lembre-se sempre: zeros têm inclinações positivas a partir da frequência de quebra e polos têm inclinações negativas. Vamos representar esse termo com uma linha vermelha:
Passo 4
Agora vamos representar os polos. Essa função de trnsgerÊncia tem três polos. Os polos tem razaõ de amplitude igual a em baixas frequências e começam a decair a uma taza de quando atingem a frequência de quebra. Para a função de transferência do exercício as função de quebra são , e e nós vamos representar esses polos com linhas azul, amarelo e laranja, respectivamente:
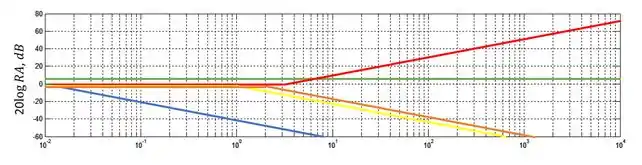
Agora só precisamos somar todas as linhas:
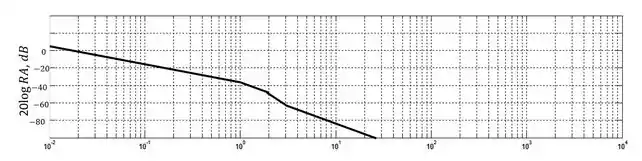
O diagrama começa em que é o valor da constante inicial. Ele tem inclinação negativa de desde o início devido ao polo na origem. Em os efeitos do segundo polo surgem e a inclinação passa a ser de . Em o terceiro polo também começa a se manifestar e a reta fica mais acentuada ainda com inclinação . Entretanto, em começa-se a sentir o efeito do zero, e a inclinação da curva volta a ser de
Resposta