Esboce o diagrama de Bode da função de transferência abaixo:
Passo 1
Nessa função de transferência temos três polos e um zero e todos já estão no formato , então já podemos partir direto para a substituição:
Vamos escrever então a expressão para a razão de amplitude (em ):
Portanto:
E o ângulo de fase:
Passo 2
Começando pela razão de amplitude.
Essa função de transferência apresenta três polos. Os polos têm razão de amplitude em baixas frequência e em altas frequências eles decaem a uma taxa de . As frequências de quebra são , e . Vamos representar esses três polos então:
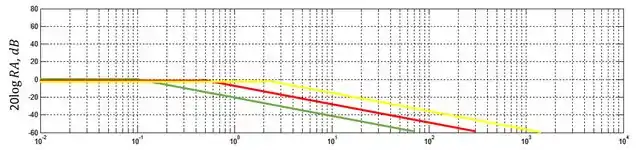
Passo 3
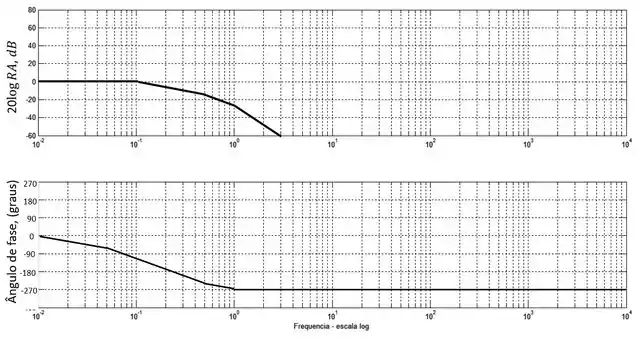
Agora só precisamos somar as três curvas:
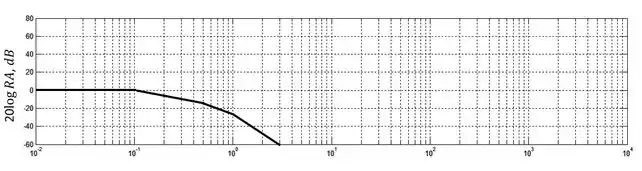
A curva de razão de amplitude começa em , a partir da primeira frequência de quebra ela começa a decair a , depois da segunda ela passa a decair a e por fim, quando ultrapassa que é a última frequência de quebra a inclinação da curva dica .
Passo 4
Agora vamos olhar para o ângulo de fase:
Vamos usar as mesmas cores que usamos para a razão de amplitude. O ângulo de fase de um polo é em baixas frequências e em altas frequências. Vamos representar o ângulo de fase para os três polos então:
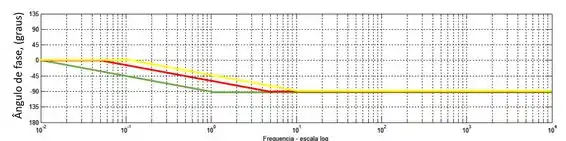
A transição entre o valor do ângulo de fase em baixa frequência para o ângulo de fase em alta frequência começa uma década antes da frequência de quebra e vai até uma década depois, gerando assim uma reta com inclinação .
Vamos somar as três linhas então:

Entre e só temos os efeitos do decaimento do ângulo de fase de um polo. A partir de o segundo polo começa a fazer efeito e a inclinação da curva fica . Em o efeito do primeiro polo para de ser sentido pois ele se torna uma constante, mas nesse ponto começa-se a se sentir o efeito do terceiro polo, e por isso a inclinação da reta permanece inalterada. Em o segundo polo ta,bém se torna uma constante e a inclinação da reta é reduzida pela metade, e em o terceiro polo também para de ser sentido e a partir daí demos uma reta constante.
Resposta