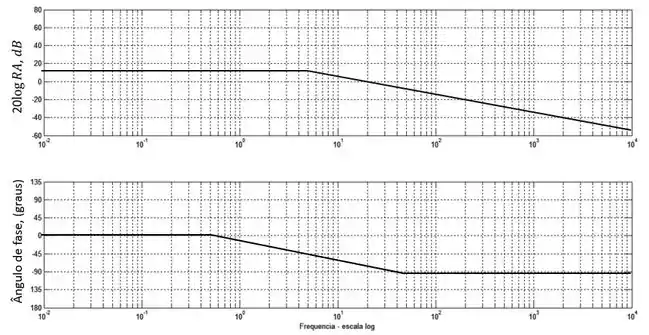
Esboce o diagrama de Bode da função de transferência abaixo:
Passo 1
Primeiramente vamos dividir toda a função por para conseguir aquele “mais um” no denominador:
Vamos escrever então a expressão para a razão de amplitude (em ):
Portanto:
E o ângulo de fase:
Passo 2
Vamos começar pela razão de amplitude.
O primeiro termo é uma constante, portanto será uma linha horizontal no diagrama de Bode, vamos representa-lo com uma linha verde:
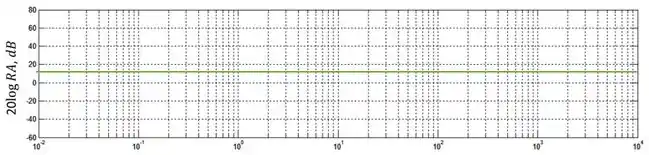
Passo 3
Já o segundo termo:
Em frequências muito baixas será uma constante de valor , e em frequências altas será uma reta com inclinação (sabemos que a inclinação é negativa por causa do sinal, mas você pode guardar que sempre que um termo estiver no denominador da função de transferência, sua inclinação será negativa). O ponto de encontro entre esses dois intervalos será na nossa frequência de quebra que nesse caso é . Vamos represetar esse termo com uma linha vermelha.
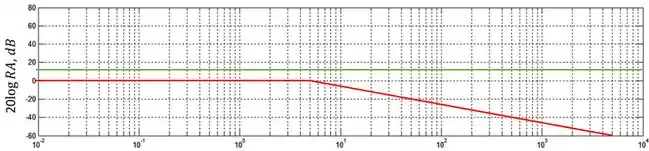
Passo 4
Somando as duas parcelas:
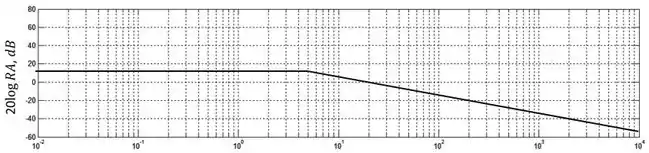
Passo 5
Agora vamos trabalhar com o ângulo de fase:
Repare que em frequências muito baixas o ângulo de fase será , e em frequências muito altas, será . A mudança entre essas duas fazes acontece uma década antes e vai até uma década depois da frequência de quebra, que nesse caso é . Sendo assim:
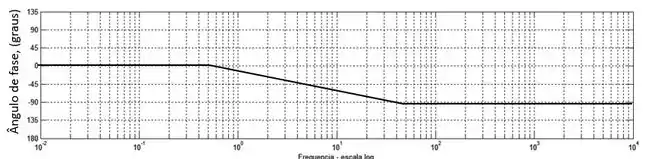
Resposta