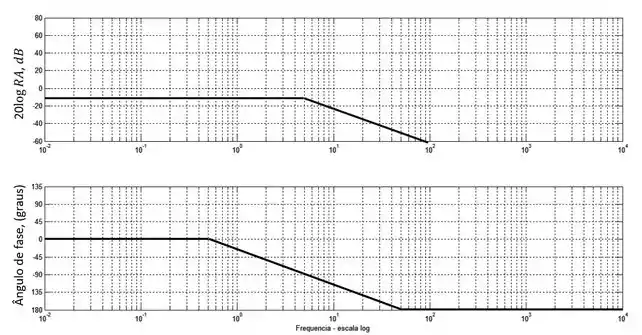
Esboce o diagrama de Bode da função de transferência abaixo:
Passo 1
Nessa função de transferência temos dois polos e um zero, nosso primeiro passo será transformar todos na forma . Então
Para calcular a razão de amplitude e o ângulo de fase, precisamos substituir por :
Vamos escrever então a expressão para a razão de amplitude (em ):
Portanto:
E o ângulo de fase:
Passo 2
Começando pela razão de amplitude.
Para representar a razão de amplitude da função de transferência, devemos representar cada termo separadamente e depois somar tudo. O primeiro termo é uma constante e será representado por uma linha verde:
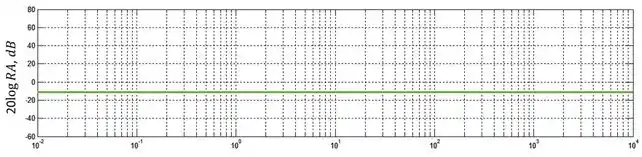
Passo 3
Além da constanste, temos também um termo referente ao polo. Os polos são em frequência muito baixa e na frequência de quebra eles se tornam uma reta com inclinação negativa. Como polo da função de transferência está elevado ao quadrado, ao invés de uma inclinação de , a reta terá inclinação a partir da frequência de quebra que é . Vamos representar esse termo com uma linha vermelha:
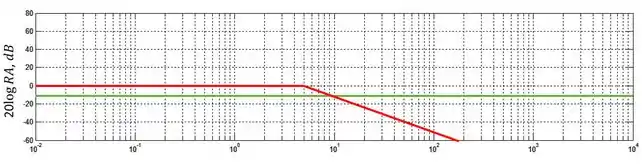
Passo 4
Agora, só precisamos somar as duas linhas:
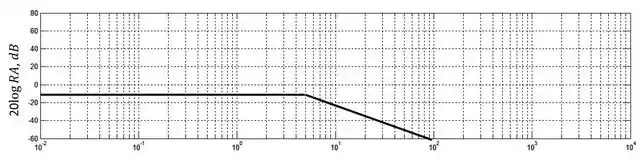
Passo 5
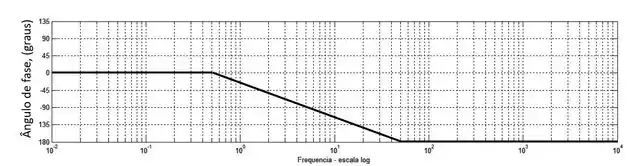
Agora o ângulo de fase:
Como só temos um termo, não precisamos esboçar cada termo separadamente e depois somar, podemos fazer diretão.
Como temos um polo de grau , em frequências muito baixas o ângulo de fase será e em frequência altas será . A transição começa uma década antes da frequência de quebra e termina uma década depois da frequência de quebra que é , gerando uma reta com inclinação .
Resposta