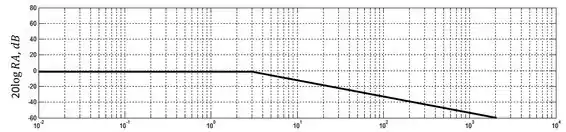
Esboce o diagrama de Bode da função de transferência abaixo:
Passo 1
Nesse caso nós temos um zero de primeira ordem e um polo de segunda ordem, nosso primeiro passo será transformar todos na forma . Então
Para calcular a razão de amplitude e o ângulo de fase, precisamos substituir por :
Vamos escrever então a expressão para a razão de amplitude (em ):
Portanto:
E o ângulo de fase:
Passo 2
Começando pela razão de amplitude.
Para a expressão da razão de amplitude temos dois termos, o primeiro referente ao zero da função de transferência e o segundo referente ao polo.
O termo do zero é um termo comum, de primeira ordem, com frequência de quebra em . Vamos representar esse termo com uma linha verde:
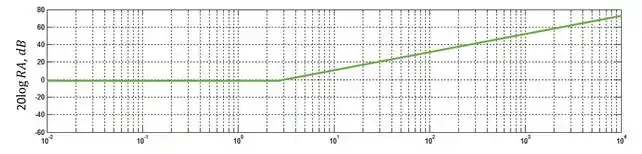
Passo 3
Já o segundo termo, referente ao polo da função de transferência, é um termo de seguda ordem. A frequência de quebra nesse caso será . Ou seja, no mesmo ponto do zero. Como se trata de um polo, a inclinação será negativa e por ser de segunda ordem, a inclinação será . Vamos representar o polo com uma linha vermelha:
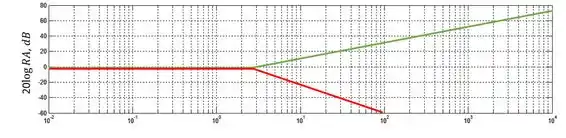
Passo 4
Agora só precisamos somar as duas linhas as linhas. Até o ponto em que ambas as linhas apresentam razão de amplitude . Nesse ponto, começamos a ter a influência de um zero que contribui com uma reta e de um polo que contribui com . Portanto, a partir de a razão de amplitude total começará a decais a uma taxa de .
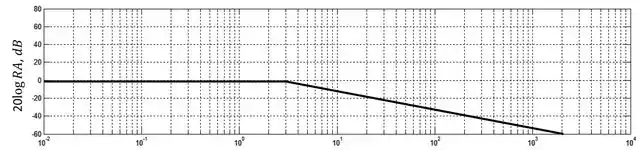
Passo 5
Vamos passar agora para o ângulo de fase:
O ângulo de fase referente ao zero, é em baixas frequências e em altas frequências. Já o ângulo referenre ao polo, também é em baixas frequências porém é em altas frequências porque é um polo de segunda ordem. O sinal negativo é devido ao fato de se tratar de um polo e não de um zero. Representando no gráfico com as mesmas cores que usamos para a razão de amplitude, temos:
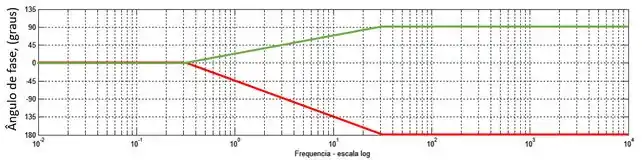
A transição entre o ângulo de baixas frequências e o ângulo de altas frequências começa uma década antes da frequência de quebra, que é para ambas as curvas, e vai até uma década depois da frequência de quebra.
Agora só precisamos somar as duas curvas:
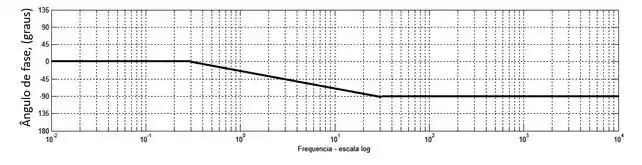
Resposta