Uma amostra, de determinado produto de moagem, apresentou a seguinte análise de peneiras:
![]()
Pede-se:
Calcular o diâmetro médio de Sauter da amostra com base em
Passo 1
Temos que calcular o diâmetro médio de Sauter de uma amostra e para isso nos foi dada uma tabela relacionando números Mesh Tyler com massas de amostra. Já extraí a informação de Mesh Tyler e transformei na informação de e , através da tabela que relaciona essas duas informações lá na teoria.
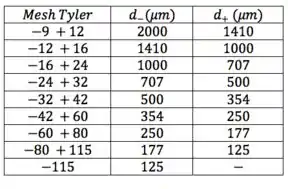
O que tem de novo nessa questão é que ela não relaciona, diretamente, as frações de massa num intervalo com os diâmetros limite do intervalo ( e ). Temos que calcular. Para isso, precisamos saber a massa total de amostra e aí pode ver qual a fração de amostra em cada intervalo.
Fora isso, é igual a fórmula que já vimos para diâmetro médio de Sauter:
Passo 2
Bora somar as massas de todos os intervalos:
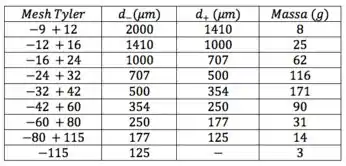
De posse da massa total, calculamos a fração de massa, ,em cada intervalo:
Pro primeiro intervalo, por exemplo:
Daí, adicionando uma coluna pros :
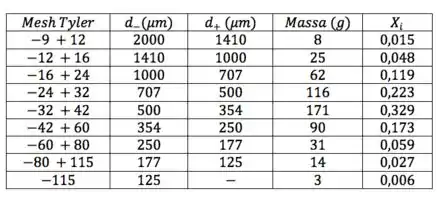
Passo 3
Vamos, também, precisar da média aritmética dos diâmetros limites de cada intervalo, isto é, . Para o primeiro intervalo, por exemplo, vai ficar:
E teremos que fazer essa conta até o penúltimo intervalo.
“Mas e o último intervalo? Só tem um dos limites do intervalo, que no caso é o , como faço?” Sempre que só tiver um dos limites, você diz que a média é ele próprio. Faz sentido: a média de um número só é ele mesmo. Daí, bora adicionar uma coluna para os :
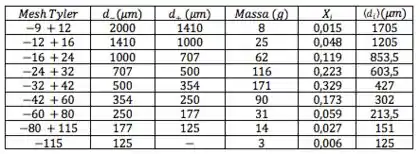
Show! Agora já temos uma relação entre e . Só eles importam agora:
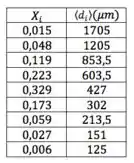
Passo 4
Agora é só jogar tudo na fórmula e calcular:
Como eu já disse, prefiro calcular o somatório separado e depois voltar pra fórmula:
Voltando pra fórmula: