A peneiração de uma amostra de areia gerou a seguinte distribuição de tamanhos:

Pede-se:
- Calcular o diâmetro médio de Sauter da amostra, com base no modelo GGS.
Passo 1
Temos uma tabela com pares (), com diâmetros em , e vamos ter que calcular o diâmetro médio de Sauter com base no modelo GGS, que é um dos modelos que vimos pra descrever a curva em função de . Daí, como está envolvendo , vamos ter que usar a fórmula para diâmetro médio de Sauter que envolve também, que é essa aqui:
Vamos ter que isolar o diâmetro na equação para e lançar nessa fórmula. Mas primeiro de tudo, precisamos da equação pra . Então bora lá:
Passo 2
Temos que calcular a equação pra pelo modelo GGS, que tem a cara:
Para estimar os parâmetros e , vamos precisar dessa equação linearizada e depois fazer regressão linear, lembra? Como vimos lá no tópico “Distribuição de Tamanhos”, a forma linearizada do GGS fica:
E, comparando com a equação genérica de uma reta, :
Portanto, vamos precisar lançar, num gráfico, versus . Bora construir, então, uma tabela com os valores. Mas não esquece que os valores de precisam estar em base unitária!!!

E, também, temos que desprezar pontos com e pontos com quando vamos fazer linearizações. Daí bora sumir com esse último ponto aí logo:

Agora sim bora achar os pares ():
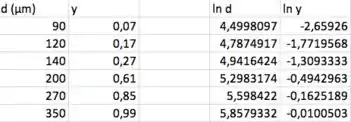
Fazendo a regressão linear com os pares ():
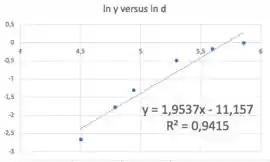
Lembrando que:
Daí:
Substituindo o valor de nessa segunda equação e cortando os “menos”:
Daí, escrevendo nossa equação de :
Passo 3
Bora agora calcular o diâmetro médio de Sauter:
Vamos precisar de , ou seja, em função de ; temos . Daí, temos que isolar o na fórmula do :
Elevando os dois lados a , isto é, :
Rearranjando:
Agora é só jogar isso na fórmula do diâmetro de Sauter:
Gosto pessoal: eu prefiro resolver a integral separado a ir levando no denominador. Acho mais fácil pra pra enxergar sei lá haha. Se preferir ir de uma vez só, de boas também.
Voltando pra fórmula do diâmetro médio: