Deseja-se peneirar areia, , no sistema de peneiras vibratórias esquematizado. Pede-se:
- Determinar o diâmetro médio de Sauter da areia com base em
- Determinar a produção de em e o diâmetro médio de Sauter de cada uma das frações com base em
Passo 1
Nessa questão, temos uma alimentação que passa por 2 peneiras e dá origem a 3 correntes. E queremos saber a vazão e os diâmetros médios de Sauter. Então, precisamos usar também os conceitos de peneiração!
Como vamos precisar calcular diâmetros médios, vamos precisar de informação de diâmetros e, por isso, temos que converter para diâmetro. Além disso, o enunciado pede pra calcular os diâmetros médios de Sauter por , daí, vamos ter que usar a seguinte fórmula:
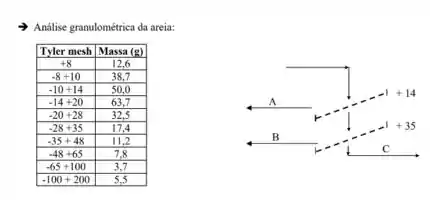
Bora então nos organizar. Vamos ter que adicionar a tabela: . Para a conversão de para diâmetros, temos que usar aquele tabelão que tá lá na teoria e para calcular os , temos que usar:
Então bora calcular o a massa total, :
Daí a primeira linha, por exemplo, vai ter :
Montando nossa tabela:
Dois comentários que eu queria fazer a respeito dessa tabela são:
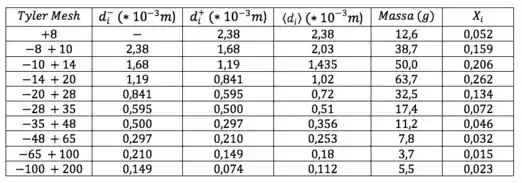
- Repara que eu coloquei, na tabela, os diâmetros em milímetro (). Fiz isso pra gente não ficar sempre só colocando diâmetros em micra (). Sei que é algo meio bobo, mas uma unidade que você nunca usou pode acabar confundindo na hora da pressa na prova
- Na hora de calcular o na primeira linha, só temos uma informação de diâmetro (relativo ao ). Não tem nenhuma outra informação sobre algum outro diâmetro para essa faixa, então usamos
Agora, bora resolver o que o enunciado pede : )
Passo 2
- Determinar o diâmetro médio de Sauter da areia com base em
- Determinar a produção de em e o diâmetro médio de Sauter de cada uma das frações com base em
É só aplicar fórmula.
Eu prefiro trabalhar com o somatório em separado e depois juntar:
Repara que eu coloquei em evidência o porque ninguém merece ficar repetindo isso vezes né? Haha Voltando pra fórmula de :
Passo 3
Vamos por etapas: primeiro calculamos as produções e depois pensamos em diâmetros médios para essas faixas, ok?
A primeira peneira é de , daí ela retém todas partículas de pra baixo, ou seja, retém as partículas de diâmetro pra cima. O que tiver diâmetro menor do que isso, passa por essa peneira de 14. Então, a corrente vai ser composta de partículas de diâmetros pra cima.
Já a peneira retém as partículas com de pra baixo, lembrando que só está indo pra essa segunda peneira o que passou pela peneira. Ou seja, a corrente vai ser composta por partículas de diâmetro entre e . E o que passa por essa peneira vai para a corrente .
Igual fizemos no exercício anterior, bora destacar na tabela, com diferentes cores, o que vai pra cada corrente, ok?

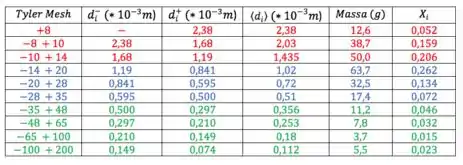
Numa prova, você não vai ter como mudar a cor da tabela, mas aconselho você destacar de alguma forma essas faixas, de boas? Circula ou faz chaves, por exemplo.
Já dividimos a tabela e sabemos quais frações vão para quais correntes. Agora é só somar as frações parciais para achar a fração total de cada corrente e multiplicar pela vazão, que é , para saber a vazão de cada uma das correntes . Assim, olha:
Daí a vazão da corrente , que vou chamar de , vai ser:
Da mesma forma, a gente calcula as vazões de :
E para :
Passo 3
Agora só falta calcular os diâmetros médios de cada uma das frações A, B e C. Vamos com atenção. Bora relembrar a forma genérica para diâmetro médio de Sauter baseado em frações parciais.
MASSSSSSSSS os que vamos usar para calcular aqui NÃO são os mesmos que estão naquele tabelão que a gente fez. Temos que considerar as frações de cada corrente. Tipo, é como se você estivesse recebendo três problemas diferentes. Bora ver o caso do que vai ficar mais claro.

Qual a massa total dessa amostra que “inventamos”?
Daí a fração relativa a massa de é:

Os são os mesmos, já que não é porque a partícula mudou de corrente que o tamanho dela muda, certo? Daí calculando o diâmetro médio de Sauter para a fração A, que vou chamar de :
Eu sei que você já sabe que eu prefiro fazer o somatório em separado, mas resolvi fazer tudo junto aqui pra não ficar mais enrolado haha
Para a corrente , é como se tivesse:

Para calcularmos os , precisamos calcular a massa total dessa amostra que inventamos:
Calculando as frações :

E o diâmetro médio para essa corrente é:
Para a corrente :

Calculando as frações :

Resposta
- ,
,
,