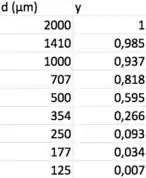
Dada a amostra abaixo, calcule o diâmetro médio de Sauter da amostra. Utilize o modelo Sigmóide para os seus cálculos.
Passo 1
Nessa questão, temos que calcular o diâmetro médio de Sauter da amostra. Para isso, nos foi dada uma tabela com pares (), daí, já dá pra notar que vamos ter que usar:
Mas antes, vamos ter que encontrar a expressão de , isto é, a expressão de em função de . Depois, colocamos e aí substituímos na integral. E o enunciado pediu pra usarmos o modelo Sigmóide para achar a curva . Daí, ela vai ter essa cara:
Passo 2
Bora lá. Primeiro de tudo, temos que achar a expressão para e, para isso, vamos precisar da forma linearizada do modelo para fazer regressão linear e achar os parâmetros:
Comparando com a equação de uma reta, :
Vamos montar uma tabela com os valores de e , mas antes disso, lembre que desprezamos pontos com ou . Então corta logo esse primeiro ponto:
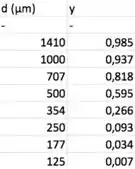
Agora sim, bora montar a tabela com e :
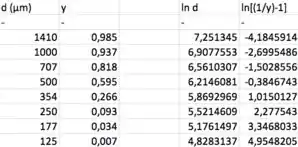
Fazendo a regressão linear de :
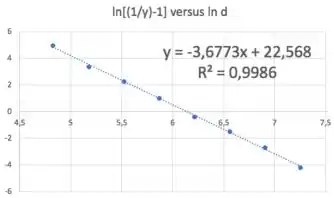
Agora podemos calcular os parâmetros do modelo Sigmóide:
Substituindo o valor de :
Daí, fica:
Passo 3
Já temos , mas precisamos de para conseguir calcular o diâmetro médio de Sauter. Daí, temos que isolar .
Invertendo os dois lados:
Jogando o para esquerda:
Elevando os dois lados a , isto é, :
Isolando e calculando :
A expressão é feia mas é essa aí haha
Passo 4
Agora é só jogar na expressão do diâmetro médio de Sauter e calcular.
Eu calculo a integral em separado, aí:
E é nessa hora que valorizamos a nossa calculadora hahah Dá pra resolver a integral na mão, mas, na prova, provavelmente o tempo vai ser corrido então aconselho ir se familiarizando com sua calculadora.
Voltando pra fórmula de :