Um cubo de aresta encontra-se em equilíbrio, flutuando na água, sabendo-se que a massa do cubo vale determine a altura submersa do cubo
Passo 1
Fala ai! Bora pra mais uma questão de empuxo! Ihuuu
Bom o enunciado da pra gente que:
Vamos considerar também a densidade da água, que é sempre bom ter no fundo da memória:
Mas como tudo está em e vamos fazer ! Para fazer essa conversão, basta dividir por , então temos que
Passando temos
ps. Se você preferir pode passar tudo para também, só que assim fica mais fácil que não fica com muitas vírgulas 😊
Passo 2
Shoooow de bola, ele quer a altura submersa, fazendo nosso diagrama de forças, temos isso daqui:
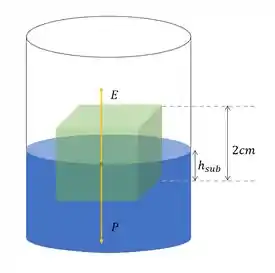
Então, como o cubo está em repouso, podemos perceber que:
Passo 3
Bora calcular o Peso primeiro
Passo 4
Show, vamos para o empuxo agora!
Vambora então!
e a gente sabe, o que falta é o volume submerso do cubo, vamos usar:
Lembrando que aqui a altura não é igual às arestas!
Show, agora vamos colocar isso na fórmula do empuxo
Passo 5
Show, agora é só igualar! Lembrando que nossas unidades estão todas iguais
Isso da pra gente