Em um recipiente com água é colocado um cubo de madeira de densidade igual a . Sabe-se que o cubo permanece em repouso e que ele possui aresta igual a Qual deve ser a altura da parte submersa do cubo? (Dado )
Passo 1
Faaaaala galerinha! Vamos pra mais uma questão sobre empuxo!
O enunciado diz que temos um cubo com essas especificações:
Também temos que:
E ele quer da gente a altura submersa! Se você está com dificuldade de visualizar isso daí, se liga nessa figura aqui:
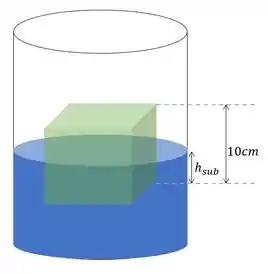
Passo 2
Belezinha, já entendemos o que está acontecendo, então vamos começar a botar a mão na massa!
Vamos fazer o diagrama de forças no bloco, teremos
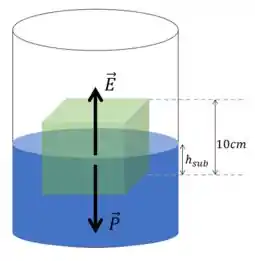
O enunciado diz que o sistema está em repouso, então essas forças tem que se anular, ou seja, uma tem que ser igual a outra
Passo 3
Para facilitar a nossa vida, vamos passar todas as unidades para o SI, ou seja, temos que passar para e para . Começaremos com a aresta do cubo
Para passar para metros temos que dividir por
Agora a densidade
Para passar para precisamos multiplicar por
Pronto, agora trabalharemos com esses valores.
Vamos começar calculando o peso!
“Mas pera lá, o enunciado não fala nada de massa pra gente!” Verdade, para isso vamos usar as informações que ele nos deu, com ela vamos usar a formulinha
O volume do cubo é
(isso porque é um cubo, as arestas são iguais, é como se fosse
Esse é a mesma coisa que multiplicar o por ele mesmo vezes
Então o volume do cubo é
Como agora sabemos que a densidade do cubo é
Vamos substituir na fórmula para achar a massa!
E fazendo essa multiplicação encontramos
Agora que temos a massa podemos, finalmente calcular a força Peso!
E sabemos que
Passo 4
Agora para o empuxo, temos que
Vambora então!
e a gente sabe, o que falta é o volume submerso do cubo, vai ser bem parecido com o volume anterior, vamos usar:
Lembrando que aqui a altura não é igual às arestas! A altura que utilizaremos é o tamanho que ficou submerso
Vamos ver as informações que colocaremos na fórmula do empuxo
Mas temos que passar a densidade da água para o SI. Lembra como passa para ? Isso aí, só multiplicar por
Agora sim podemos pegar a fórmula do empuxo
E substituir os valores
E multiplicando todo mundo, teremos
Passo 5
Por último é só igualar o empuxo com o peso, que nem vinos no Passo , para acharmos
Como já calculamos o peso como sendo , substituindo
Podemos passar o para o outro lado da equação dividindo
E ficamos com
Só que as respostas estão em , então temos que converter de metros para centímetros. Para fazer isso, basta multiplicar o número por
Pronto! Encontramos a altura submersa do cubo! 😊
Resposta
b)