Uma massa de tem uma certa velocidade . Sua energia cinética será:
A.
B.
C.
D.
E.
Passo 1
Deixa eu advinhar, essa velocidade em formato de vetor te deixou preocupado?
Não fica, vamos fazer juntos e vou te mostrar que é moleza. Vamos começar entendendo o que o vetor velocidade significa. Ele tem a forma:
Colocando em forma gráfica:
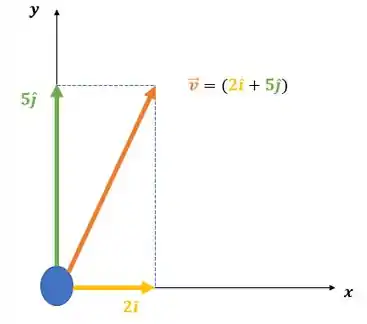
Ou seja, a velocidade é formada pela componente no eixo e pela componente na direção do eixo .
Percebe que as componentes e o vetor velocidade formam um triângulo retângulo:
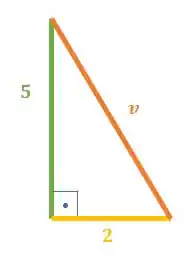
Pelo Teorema de Pitágoras, nós sabemos que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Mas quem são os catetos e quem é a hipotenusa?
Bom, os catetos são os lados que formam o ângulo de :
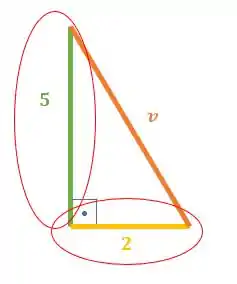
Enquanto a hipotenusa é o lado oposto ao ângulo de :
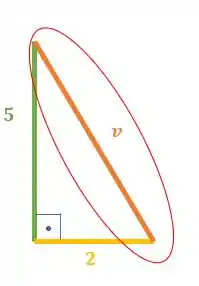
Colocando essas informações sobre os catetos e e a hipotenusa no Teorema de Pitágoras:
Elevando ao quadrado e ao quadrado, nós temos:
Logo, o cálculo da velocidade ao quadrado é igual a:
Não vamos tirar a raiz quadrada por enquanto, vamos guardar esse valor com carinho e pensar no resto do problema.
Passo 2
Opa!! Se ele tá pedindo a energia cinética e te dá a massa e a velocidade aí a gente pode ficar tentado a só jogar tudo na fórmula da energia cinética...
Mas, porém, contudo, todavia, entretanto temos que ter atenção a uma coisinhas!
A massa deve estar em . Vamos resolver esse probleminha:
Em relação a massa:
Passando pra devemos dividir o valor por :
Passo 3
A energia cinética é dada por:
Nós já calculamos o valor da massa e da velocidade ao quadrado, lembra? Eles eram:
Então vamos substituir esses valores na fórmula:
Multiplicando por , encontramos:
Dividindo por enconstraremos o valor final da energia cinética:
Resposta
Alternativa D