Um elétron, com massa de repouso e energia cinética colide com um pósitron em repouso produzindo dois fótons, conforme ilustrado na figura abaixo. O pósitron é uma partícula com a mesma massa de repouso do elétron, porém com carga oposta.
Determine o comprimento de onda dos fótons em função de e .
Encontre o ângulo de espalhamento.
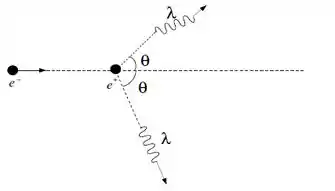
Passo 1
Letra : Para resolver este item, utilizaremos a conservação de energia. Como se trata de uma colisão entre partículas elementares (elétron e pósitron) criando fótons, temos então que considerar a colisão com sendo relativística. Deste modo, a equação para conservação de energia é
parado e o elétron colidindo com o pósitron com energia cinética . Deste modo, temos que
Depois da colisão, temos dois fótons com mesmo comprimento de onda . Deste modo,
onde usamos a relação . Note que os fótons não possuem energia de repouso.
Deste modo, substituindo na equação de conservação de energia,
Passo 2
Letra : Para resolvermos este item, utilizaremos a conservação de momento linear. Este princípio nos diz que
Inicialmente, o pósitron está parado e o elétron colide com o pósitron com um certo momento na direção . Veja a figura abaixo que mostra antes da colisão.
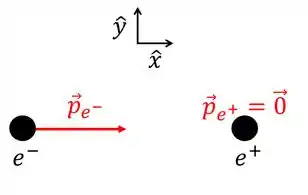
Posteriormente, temos dois fótons cujos momentos e fazem um ângulo com a direção . Veja a figura a seguir.
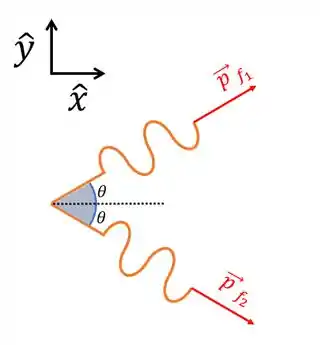
Como a equação de conservação de momento é uma equação vetorial, devemos analisá-la em cada direção (x e y). Veremos isto no passo seguinte.
Passo 3
Vemos que na direção , a equação de conservação de momento é
Já na direção , a equação de conservação de momento retorna
Desta última equação, como , podemos concluir rapidamente que e
Sendo assim, a equação de conservação de momento na direção se torna
Utilizando a relação de de Broglie , com o comprimento de onda dos fótons, temos que
Isolando o ângulo e utilizando o resultado do item , temos que
Ainda precisamos determinar . Isto será realizado no próximo passo.
Passo 4
Para determinarmos , utilizaremos a equação da energia do elétron antes da colisão . Sabemos que e se relacionam por
Deste modo, sabendo que , obtemos queFinalmente, substituindo na expressão para , temos que