(Adaptada) Água escoa em regime permanente através de um cotovelo redutor, conforme mostrado. O cotovelo é liso e curto e o escoamento acelera, de modo que o efeito do atrito é pequeno. A vazão em volume é . O cotovelo está em um plano horizontal. Calcule a componente x da força exercida pelo cotovelo redutor sobre o tubo de suprimento de água.
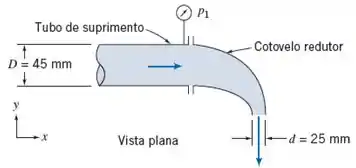
Dados: pressão manométrica na seção 1 é .
Passo 1
Vamos ao primeiro passo que é escolher o volume de controle (VC). Queremos saber a componente x da força exercida pelo cotovelo redutor sobre o tubo, logo, o VC precisa passar pela conexão tubo-cotovelo.
Além disso, temos informações sobre a saída do cotovelo, então é interessante que o VC passe por lá.
O toque final é deixar esse volume de controle o mais simétrico possível. Com isso, olha só quem foi escolhido:
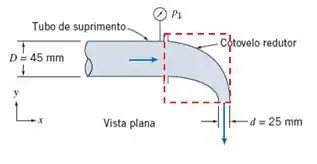
Passo 2
Hora de aplicar a equação da conservação do momento linear! O enunciado pede a componente x da força, então vamos analisar a equação na direção x, beleza?
Fazendo as hipóteses de escoamento permanente, fluido incompressível e propriedades uniformes, podemos usar essa equação:
Repara que u é a componente da velocidade em x. Na saída do cotovelo, a velocidade está somente no eixo y, logo
E qual seria a velocidade de entrada? O cotovelo está no plano horizontal e pela figura, podemos perceber que na entrada do VC:
Ok! Mas quem é , não é mesmo? Então, vamos conseguir calcular a velocidade de entrada pela vazão volumétrica e diâmetro do tubo que o enunciado deu. A conta é essa aqui:
Lembrando de converter as unidades para o SI: e :
Então, a componente da velocidade de entrada em x é
Para encontrar a vazão mássica, podemos usar a seguinte relação já que assumimos a hipótese de fluido incompressível (água)
Substituindo
Agora a pergunta que não quer calar... Quais forças atuam no eixo x?
Temos a força do tubo sobre o cotovelo , além da força de pressão do fluido na seção 1 :
Lembrando que
E
Utiliza-se a pressão manométrica, pois a pressão atmosférica atua de forma simétrica. Assim:
Essa é a força exercida pelo tubo sobre o cotovelo. Para achar, a força exercida pelo cotovelo redutor sobre o tubo, (reação) trocamos o sinal.
Resposta
A força exercida pelo cotovelo redutor sobre o tubo é